Raziskovalni matematični seminar - Arhiv
| 2026 | 2025 | 2024 | 2023 | 2022 | 2021 | 2020 | 2019 | 2018 | 2017 | 2016 | 2015 | 2014 | 2013 | 2012 | 2011 | 2010 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
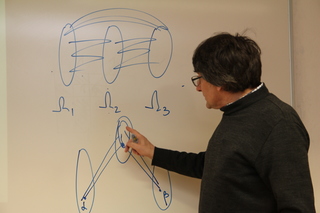
In 2003, Boros and Gurvich proved that a chess-likes game has a Nash equilibrium (NE) in pure stationary strategies if (A) the number n of players is at most 2, or (B) the number p of terminals is at most 2 and (C) any infinite play is worse than each terminal for every player. In the talk we strengthen the bound in (B) replacing p <= 2 by p <= 3, provided (C) still holds. On the other hand, we construct an NE-free four-person chess-like game with five terminals, which has a unique cycle, but does not satisfy (C). It remains open whether an NE-free example exists for n = 3, or for 2 < p < 4, or for some n > 3 and p > 4 provided (C) holds.
Joint work with E. Boros, V. Oudalov, and R. Rand.

Motivated by challenges related to domination, connectivity, and information propagation in social and other networks, we study the Vector Connectivity problem. This problem takes as input a graph G and an integer r(v) for every vertex v of G, and the objective is to find a vertex subset S of minimum cardinality such that every vertex v either belongs to S, or is connected to at least r(v) vertices of S by disjoint paths. If we require each path to be of length exactly 1, we get the well-known vector domination problem, which is a generalization of the dominating set and vertex cover problems. Consequently, the vector connectivity problem becomes NP-hard if an upper bound on the length of the disjoint paths is also supplied as input. Due to the hardness of these domination variants
even on restricted graph classes, like split graphs, Vector Connectivity seems to be a natural problem to study for drawing the boundaries of tractability for this type of problems.
In the talk, we will give an overview of known complexity results for the Vector Connectivity problem. In particular, the problem can be solved in polynomial time on split graphs, in addition to cographs, trees, and block graphs. On the other hand, the problem is NP-hard for planar line graphs and for planar bipartite graphs, APX-hard on general graphs, and can be approximated in polynomial time within a factor of log n + 2 on all n-vertex graphs. Vertex covers and dominating sets in a graph G can be easily characterized as hitting
sets of derived hypergraphs (of G itself, and of the closed neighborhood hypergraph of G, respectively). Using Menger's Theorem, a similar characterization of vector connectivity sets can be derived.
Based on joint works with Endre Boros, Ferdinando Cicalese, Pinar Heggernes, Pim van 't Hof, and Romeo Rizzi.
Download slides!
Interpolation of curves and surfaces is a fundamental problem in computer aided
geometric design (CAGD) and related fields of research. In this talk we shall
focus on interpolation of parametric curves (or data) by parametric polynomial
curves. In contrast to functional case, where a polynomial of degree n can, in
general, interpolate at most n+1 points, planar parametric polynomial curve of
degree n might interpolate as much as 2n points. This kind of interpolation is
known as ’geometric interpolation’. Some results and open problems related to
geometric interpolation will be presented and interpolation of special parametric
objects (such as circular arcs) will be briefly outlined.
Download slides.
A signed graph is pair (G,s) where G is a graph and s, the signature, is a function on the edges of G assigning values in {1,-1}. Similarly to simple unsigned graphs, it is possible to associate several graph matrices and to study the signed graphs from a spectral viewpoint. A common problem in Spectral Theory of unsigned graphs is to consider special families of graphs and to study whether each graph in the family is determined by the spectrum of the corresponding graph matrix. Namely, a graph is determined by the spectrum if and only if any other cospectral graph is isomorphic as well. In this seminar we extend the latter concept to signed graphs and as an example we will show that the signed Lollipop graph is determined by the spectrum of its Laplacian matrix.
This is a joint research with Pawel Petecki.
Recently, Milanič and Trotignon introduced the class of equistarable graphs as graphs without isolated vertices admitting positive vertex weights on the edges such that a subset of edges is of total weight 1 if and only if it forms a maximal star. Based on equistarable graphs, counterexamples to three conjectures on equistable graphs were constructed, in particular to Orlin's conjecture, which states that every equistable graph is a general partition graph.
In the talk we characterize equistarable bipartite graphs.
We show that a bipartite graph is equistarable if and only if every 2-matching of the graph extends to a matching covering all vertices of degree at least 2. As a consequence of this result, we obtain that Orlin's conjecture holds within the class of complements of line graphs of bipartite graphs.
We also connect equistarable graphs to the triangle condition, a combinatorial condition known to be necessary (but in general not sufficient) for equistability. We show that the triangle condition implies general partitionability for complements of line graphs of forests, and construct an infinite family of triangle non-equistable graphs within the class of complements of line graphs of bipartite graphs.
This is a joint work with Martin Milanič and Endre Boros.
Download slides!
We implemented several programs that may deal with general Haar graphs. The programs are written in Python but embedded in the system sage. A Haar graph is a covering graph over a dipole. This means it can be described by a set
S of voltages where each element s from S is assigned to one of the one of the arcs leading from a black vertex of a dipole to a white vertex of a dipole with k edges, such that |S| = k and each arc receives its voltage. Here S is a set taken from some group G. If X is a set on n vertices, then each faithful X-action of G gives rise to a derived graph H(S,G,X), called the Haar graph. In paractice only two actions are considered:
1. G is a subgroup of the symmetric group Sym(X), generated by S. In this case S is simply a set of permutations of an n-set. We shorten notation to H(S) and call the derived graph a permutation Haar graph.
2. G is generated by S and acts on itself with the usual right regular action. We shorten the notation to H(S,G) and call the derived graph a G-Haar graph. In particular, the cyclic Haar graphs have been studied in the past by Hladnik, Marusic and Pisanski. Hladnik independently developed a theory that lead to the study of abelian Haar graphs.
Our system has possibility to work with special classes of Haar graphs, eg. permutation Haar graph, cyclic Haar graph and abelian Haar graphs.
We present basic properties of universal covering projections and exploit them in order to develop an algorithm for computing all solvable regular covering projections of a given graph admitting a lift of a given group of automorphisms.
Download slides!
A Cayley graph Cay(G,S) is called a CI-graph if for every subset T
of G, if Cay(G,T) and Cay(G,S) are isomorphic, then T=f(S) for some automorphism f of G. The group G is called a DCI-group if every Cayley graph of G is a CI-graph, and it is called a CI-group if every undirected Cayley graph of G is a CI-graph. Although there is a restrictive list of potentional CI-groups (Li-Lu-Pálfy, 2007), only a few classes of groups have been proved to be indeed CI; in several cases the proof was obtained by studying the Schur rings over the given group. In my talk I will review the Schur ring method.
Generalized Cayley graphs were defined by D.Marušič, R. Scapellato and N. Zagaglia Salvi in 1992. They studied properties of such graphs, mostly related to double coverings of graph. They also posed a question whether there exists a generalized Cayley graph which is vertex-transitive but not Cayley graph.
Download slides!
For a perfect graph G, and given a weight function w on the vertices of G, linear programming duality ensures that the weight of a minimum weighted clique cover (an assignment of a non-negative weight y_C to each clique C of G, such that, each vertex v is covered by cliques whose weight sums at least w(v) and that
minimizes the total sum of the weights of the cliques) is the same as the weight of a maximum weighted stable set (a set of pairwise nonadjacent vertices S that maximizes the sum of the weights). Moreover Grötschel, Lovász and Schrijver gave in 1988 a (non combinatorial) algorithm, building upon Lovász's theta function, to compute both solutions. It is a major open problem in combinatorial optimization whether there exist polynomial time combinatorial algorithms for those two problems. For particular classes of perfect graphs, such algorithms exist. This is the case, for instance, for claw-free perfect graphs (a graph is claw-free if none of its vertices has a stable set of size three in its neighborhood).
Download slides.
Chordal and dually chordal graphs are well known classes, whose duality becomes evident by the use of trees: a dually chordal graph is characterized by the existence of a tree such that every clique of the graph induces a subtreee (the compatible tree), whereas a chordal graph is characterized by the existence of a tree such that each member of the dual of the clique family induces a subtree (the clique tree).
Download slides.
The reconfiguration graph of the $k$-colourings of a graph $G$ contains as its vertex set the proper vertex $k$-colourings of $G$, and two colourings are joined by an edge in the reconfiguration graph if they differ in colour on just one vertex of $G$. We investigate the structure of reconfiguration graphs and the computational complexity of recognizing whether or not a pair of colourings belong to the same component of the reconfiguration graph (that is, the complexity of deciding if it is possible to transform one colouring into another with a sequence of ''recolouring'' steps that each change the colour on just one vertex without ever breaking the constraint that neighbours are not coloured alike).
Download slides.
V kombinatorični optimizaciji se ukvarjamo z iskanjem optimuma linearne ali kvadratične funkcije nad končno množico, ki pa je praviloma zelo velika in povezana s kakšno bazno kombinatorično množico (kombinacije, permutacije,...).
Ken Brown asked whether there is any group G such that the coset lattice of G is contractible. I'll start by telling you what this question means. I'll then describe some recent progress of myself and John Shareshian towards a negative answer.
An essential tool of our work is Smith Theory, which examines the action of a p-group on a topological space, and examines its fixed point set. As time allows, I will survey some results from this theory.
Graph theory has changed completely from the late-19th century to the late 20th century, from a collection of mainly recreational problems to a well-developed mainstream area of mathematics. In this talk I outline its development over this period, both chronologically and thematically.

Euler was the most prolific mathematician of all time – but what did he do? In this talk I survey his life in Basel, St Petersburg and Berlin, and outline some of the contributions he made to the many areas in which he worked – for the very pure to the very applied.
Exchange of information occurs on all levels of living matter, and it is the basis without which life could not be developed, especially on the level of multi cell systems. In society of animals information is communicated in a
specific way, and as far it is known it is always reliable, because it is the basis for survival of species. In human societies information as the rule is often not reliable because it is used for acquiring power and privileges, a very specific attribute of this species. Among humans information is transmitted by the word of mouth and written word.
Reliability of information is therefore at the heart of problems in organized society and the only way tool to verify is science. Central role in modern communication is played by internet, a very powerful tool, to which everybody has access to transmit any information and therefore it is of paramount importance to select reliable information. In that respect the network GEOSET was set up about which will be given description in this talk.
In the talk, I will outline several approaches to non-commutative generalizations of Stone duality that have been developed in recent years. The general idea can be very briefly explained as follows: we consider an algebra that generalizes a Boolean algebra (or a distributive lattice, or a frame) and enquire how the dual topological (localic) object of the commutative structure can be upgraded to dualize the whole algebra. We present dualities for Boolean inverse semigroups, pseudogroups and their non-involutive analogues called complete restriction semigroups. These objects are dualized by some topological (or, more generally, localic) categories or groupoids. I am also going to explain the natural role of quantales in these dualities. The talk is based on several papers authored by to Mark Lawson, Daniel Lenz, Pedro Resende and the speaker.
In equity-linked life insurance contracts, the benefits are directly linked to the value of an investment portfolio. The financial risk can be totally charged to the policyholder in pure equity-linked constracts, or it can be shared between the policyholder and the insurance company, in guaranteed equity-linked contracts (minimum guarantees are offered to the policyholder). In this talk, we will mainly focus on the latter case. Whenever the market value drops below the guaranteed sum, so called additional policy reserves (APR) are required. Since these APR are stochastic and cause additional costs for the insurance company, it is important to quantify the distribution of the APR accurantely. Results obtained by Nonnenmacher and Russ will be presented and also some possibilities for further research.
Classical covering theory ensures each connected metric space with reasonable local properties ( locally path connected, and semi locally simply connected) admits a universal covering (essentially uniquely). In this case the preimages of the natural covering map are discrete.
How might one reasonably generalize the latter facts, sacrificing discreteness of fibres and nice local properties of the base, and obtain a fibre bundle rather than a traditional covering map, whose total space is simply connected, so that all paths in the base space lift uniquely, and so that all fibres are totally disconnected?
There is no universally agreed upon definition of generalized universal cover.
However we will discuss one of the most natural definitions, see why fibre bundles are often hopeless to obtain, but present a substantial class of nontrivial examples where fibre bundles are indeed achieved. along with the other mentioned properties.
In particular, certain planar sets generate bundles whose fibres are the classical free topological groups over countably many generators in the sense of Graev or Markov.
This talk is motivated by a question of Andrej Bauer.
http://mathoverflow.net/quest

Na seminarju bodo predstavljeni nekateri novejši rezultati v zvezi z ohranjevalci na tenzorskem produktu kompleksnih matrik.
The concepts of adjacency and distance are two of the most basic terms in graph theory. A natural generalization leads to the notion of distance degree which tells us the number of vertices at some distance from the chosen vertex. When studying distance degrees we can limit ourselves to the so called distance degree regular graphs, where all the distance degrees for all the vertices are the same, and self-median graphs, where the sum of distances from a chosen vertex to all the other vertices is independent of the selected vertex. It was shown that the former correspond to strongly distance-balanced graphs while the latter correspond to distance-balanced graphs.
The talk will focus on the properties and known families of the mentioned types of graphs, the complexity of obtaining them and their use in practical applications. It will present an overview of the known results and pose some still unanswered questions.
Roughly speaking an end of a graph G(V,E) is an equivalence class of one-way infinite paths such that any two different equivalence classes can be separated from each other by removing a finite subset S of V(G). In this talk we consider infinite subsets of V(G) with certain growth rates which can be separated from each other by a connected subgraph of G with smaller growth rate. Following the ideas presented in a paper of Stallings we not only generalize the concept of ends, but also some of the well-known results about ends of graphs.
In this talk, we will consider the Hermite interpolation with PH spline curve. In particular, at each spline segment the C^1 data at two end points are interpolated by PH cubic biarc and the two arcs are joined together at some unknown common point sharing the same unknown tangent vector. The obtained biarc is expressed in a closed form with three free parameters. The problem of specifying two free angular parameters has been introduced in the literature for characterizing Hermite interpolation based on PH quintics and the strategy to determine these two parameters easily and suitably is identified by the acronym CC. We will export this strategy to our field. More precisely, we will present a method which requires only the evaluation of two analytic explicit expressions and which still guarantees that, when the PH cubic interpolant to Hermite data exists, it is reproduced by our algorithm. The asymptotic behavior of solution will be studied and the shape-preserving properties, particularly the torsion, will be presented. The resulting algorithm is implemented in Mathematica and somenumerical experiments that confirm the theoretical results will be shown.
These results were obtained during the visit of the speaker at the University of Florence last April, and are joint work with Alessandra Sestini (Università degli Studi di Firenze), Carla Manni (Università di Roma “Tor Vergata”) and Maria Lucia Sampoli (Università degli Studi di Siena).
A stable set in a graph is a set of pairwise non-adjacent vertices, and a stable set is maximal if it is not contained in any other stable set. Equistable graphs are graphs admitting positive weights on vertices such that a subset of vertices is a maximal stable set if and only if it is of total weight 1. General partition graphs are the intersection graphs of set systems over a finite ground set S such that every maximal stable set of the graph corresponds to a partition of S. It is known that general partition graphs are exactly the graphs such that every edge is contained in a strong clique (a clique is strong if it intersects all maximal stable sets).
No combinatorial characterization of equistable graphs is known. In 2009, Orlin proved that every general partition graph is equistable, and conjectured that the converse holds as well. Orlin's conjecture has been verified for several graph classes, including line graphs, simplicial graphs, very well-covered graps, chordal graphs, series-parallel graphs, AT-free graphs, EPT graphs, and certain graph products. Orlin's conjecture, if true, would imply another conjecture on equistable graphs due to Mahadev, Peled, and Sun from 1994, stating that every equistable graph is strongly equistable. A conjecture that would follow from Orlin's conjecture and would imply the conjecture by Mahadev, Peled, and Sun was posed in 2011 by Miklavič and Milanič in 2011, and states that every equistable graph has a strong clique.
In the talk, I will present an infinite family of counterexamples to Orlin's conjecture. The family contains equistable graphs not having any strong cliques, and hence also disproves the conjecture by Miklavič and Milanič.
The results were obtained jointly with Stéphan Thomassé and Nicolas Trotignon, during a recent visit of the speaker at ENS Lyon.
A decomposition $\mathcal{C}=\{ C_1,C_2,...,C_h\}$ of the complete $k$-uniform hypergraph $K^k_n$ of order $n$ is called {\em cyclic Hamiltonian} if each $C_i\in \mathcal{C}$, $i\in\{1,2,\ldots,h\}$, is a Hamiltonian cycle in $K^k_n$ and there exists a permutation $\sigma$ of the vertex set of $K^k_n$ having exactly one cycle in its cycle decomposition such that for every cycle $C_i\in\mathcal{C}$ its set of edges coincides with an orbit of $\langle\sigma\rangle$ when acting on the edge set of $K^k_n$. In this paper it is shown that $K_n^k$ admits a cyclic Hamiltonian decomposition if and only if $n$ and $k$ are relatively prime and $\lambda=\min\{d>1:\ d|n\}>\frac nk$.
A finite group G is called a Cayley integral group if every undirected Cayley
graph over G has integral spectrum. Finite abelian Cayley integral groups have
been determined by W. Klotz and T. Sander [Electronic J Combin. 17 (2010), #
R81.] In this talk we determine the finite non-abelian Cayley integral groups.
We show that if certain arithmetic conditions hold, then the Cayley isomorphism problem for abelian groups, all of whose Sylow subgroups are elementary abelian or cyclic, reduces to the Cayley isomorphism problem for its Sylow subgroups. This yields a large number of results concerning the Cayley isomorphism problem, perhaps the most interesting of which is the following: if $p_1,\ldots, p_r$ are primes satisfying certain arithmetic conditions, then two Cayley digraphs of $\Z_{p_1}^{a_1}\times\cdots\
It is well known that not every combinatorial configuration admits a geometric realization with points and lines. Moreover, some of them do not admit even realizations with points and pseudolines, i.e. they are
not topological. In this paper we show that every combinatorial configuration can be realized as a quasiline arrangement on a real projective plane. A quasiline arrangement can be viewed as a map on a closed surface. Such a map can be used to distinguish between two "distinct" realizations of a combinatorial configuration as a quasiline arrangement. Based on work in progress with several mathematicians including Leah Berman, Juergen Bokowski, Gabor Gevay, Jurij Kovič and Arjana Žitnik.