Raziskovalni matematični seminar - Arhiv

This is a presentation of the PhD thesis topic. The PhD thesis will consist of two parts: Generalized bent (gbent) functions (as a main part) and other topics related to cryptography.

Having the application in OFDM and MC-CDMA modulation techniques, which suffer from relatively high peak-to-mean envelope power ratio (PMEPR), in 2007 K. U. Schmidt proved that PMEPR is minimized if and only if a gbent function is used in OFDM/MC-CDMA systems. In the PhD thesis we will provide a full characterization of gbent functions (mappings from F^n_2--> Z_q), where we show that in algebraic sense they correspond to affine spaces of bent or semi-bent Boolean functions which satisfy certain properties related to Sylvester-Hadamard matrices.  Moreover, we introduce the notion of Z_q-bent functins (as a subclass of gbent functions) which correspond to relative difference sets/ vectorial bent functions. For even number of input variables n, we determine the dual function of a gbent function, and depending on the parity of n we will prove that Gray maps of gbent functions are plateaued Boolean functions.

Apart from related topics, we consider three problems. First, we consider the problem of optimizing the placement of tap positions in LFSR-based stream ciphers. Analyzing the GFSGA attack we provide two algorithms for taps selection. We show that our algorithms may provide a significant improvement of resistance of the LFSR-cipher (which employs a filtering function) to GFSGA-like attacks comparing to relative difference sets. In addition, two new modes of the GFSGA attack are developed.
Then, we provide an algorithm for estimating the resistance of a random Boolean function to (Fast) Algebraic attacks (for relatively large number of input variables, say n>30 -- which appears to be a hard problem).  The complexity of our algorithms is estimated as O(n^2 2^n), which is much less then previous known algorithms.
At the end, we consider the problem of finding polynomials over finite fields which cannot possess  linear structures. Such polynomials provide an optimal resistance to differential cryptanalysis. We identify several infinite classes of such polynomials, and we derive the upper bound on the degree of so-called planar mappings. 

Let S_n be the symmetric group on n letters. Given two r-tuples (a_1,a_2,...,a_r) and (b_1,b_2,...,b_r) of permutations of S_n the decision r-simultaneous conjugacy problem asks whether there is a permutation \tau in S_n which simultaneously conjugates these two tuples, that is, whether the following system of equations b_j = \tau^{-1}a_j\tau, j=1,2,...,r, over S_n has a solution. The search version of this problem is defined in the obvious manner, and is referred to as the search simultaneous conjugacy problem.

The solution of the simultaneous conjugacy problem has great potential for a variety of applications in different fields of mathematics and computer science such as automata theory, permutation groups, maps on surfaces, graph theory, representation theory, and cryptography. For example, in the language of deterministic finite automata the decision simultaneous conjugacy problem  is precisely the semiautomata isomorphism problem. The question whether two oriented maps on a closed surface are isomorphic translates to the special case of the decision simultaneous conjugacy problem for r = 2. Also, the decision problem interpreted in terms of permutation matrices is equivalent to a special case of asking whether two group representations are equivalent. An important variant of the conjugacy problem occurs when asking for all solution where a_j = b_j for all indices j; in this case we ask for the centralizer of a given set of permutations. In particular, this is encountered in finding the automorphism groups of embedded graphs on surfaces. Further, in the theory of covering graphs the question whether two covering projections are equivalent translates to the decision version of the conjugacy problem. Last but not least, the simultaneous conjugacy problem can be naturally generalised to arbitrary groups. For instance, in braid groups the search problem plays an important role in studying braid cryptographic protocols.

The best-known deterministic algorithm which solves the search version (and hence the decision version) has the \mathcal{O}(rn^2) time complexity. In addition, there are no lower bounds in the literature for the decision/search simultaneous conjugacy problem, except the trivial linear bound \mathcal{O}(rn). In the talk we present some new results which reduce the gap between the upper and lower bound. 

Joint work with Andrej Brodnik and Aleksander Malnič.

(Joint work with Zakir Deniz)

Our Turkish-Slovenian Project entitled “New Trends in Matching Theory” has started in July 2014 and will be finishing in January 1 st , 2017. We first summarize questions addressed in the framework of this project and the results obtained. We then focus on one of our most recent results about stable equimatchable graphs.

A graph G is equimatchable if every maximal matching of G has the same cardinality. We are interested in equimatchable graphs such that the removal of any edge from the graph preserves the equimatchability. We call an equimatchable graph G edge-stable if G-e is equimatchable for any e\in E(G). After noticing that edge-stable equimatchable graphs are either 2-connected factor-critical or bipartite, we characterize edge-stable equimatchable graphs. This characterization yields an O(min(n^{3.376} , n^{1.5} m)) time recognition algorithm. We also define vertex-stable equimatchable graphs and show that they admit a simpler characterization. Last, we introduce and shortly discuss the related notions of edge-critical and vertex-critical equimatchable graphs, pointing out the most interesting case in their characterization as an open question.

This is joint work with Vladislav Kabanov, Leonid Shalaginov and Alexandr Valyuzhenich.

Many combinatorial configurations (for example, perfect codes, latin squares and hypercubes, combi-
natorial designs and their q-ary generalizations — subspace designs) can be defined as an eigenfunction on a graph with some discrete restrictions. The study of these configurations often leads to the question about the minimum possible difference between two configurations from the same class (it is often related with bounds of the number of different configurations; for example, see [1–5]). Since the symmetric difference of these two configurations is also an eigenfunction, this question is directly related to the minimum cardinality of the support (the set of nonzero) of an eigenfunction with given eigenvalue. This talk is devoted to the problem of finding the minimum cardinality of the support of eigenfunctions in the Paley graphs of order q^2 (denote it by P(q^2)), where q is prime power. Currently, a similar problem is solved for Hamming graphs H(n, q) for q = 2 (see [4]). In [6] Vorob’ev and Krotov proved the lower bound on the cardinality of the support of an eigenfunction of the Hamming graph. In [7] the minimum cardinality of the support of eigenfunctions in the Hamming graphs with the second largest eigenvalue n(q − 1) − q was found.

In this talk, we present construction of eigenfuctions on P(q^2) for both non-principal eigenvalues; the cardinality of the support of the eigenfunctions is equal to q + 1. It follows from [3], that our construction gives eigenfunctions with minimum cardinality of support. As a related topic, we will discuss maximal cliques in P(q^2) of order (q + 1)/2 and (q + 3)/2, where q ≡ 1(4) and q ≡ 3(4), correspondingly. In [8], Baker, Ebert, Hemmeter and Woldar proposed contruction of such cliques, but they noted that their construction doesn’t cover all known cliques.

References

[1] E. F. Assmus, Jr and H. F. Mattson. On the number of inequivalent Steiner triple systems. J. Comb. Theory, 1(3):301-305, 1966.

[2] O. Heden and D. S. Krotov. On the structure of non-full-rank perfect q-ary codes. Adv. Math. Commun., 5(2):149-156, 2011.

[3] D. Krotov, I. Mogilnykh, V. Potapov. To the theory of q-ary Steiner and other-type trade. Discrete Mathe-
matics. 2016. V. 339, N 3. P. 1150-1157.

[4] V. N. Potapov. On perfect 2-colorings of the q-ary n-cube, Discrete Math., 2012, V. 312, N. 8, 1269-1272. [5] V. N. Potapov and D. S. Krotov. On the number of n-ary quasigroups of finite order. Discrete Math. Appl., 21(5-6):575-585, 2011.

[6] K. V. Vorob’ev and D. S. Krotov. Bounds for the size of a minimal 1-perfect bitrade in a Hamming graph. J. Appl. Ind. Math., 9(1):141-146, 2015. translated from Diskretn. Anal. Issled. Oper. 6(21):3-10, 2014.

[7] A. Valyuzhenich. Minimum supports of eigenfunctions of Hamming graphs. Accepted to Discrete Mathemat-
ics.

[8] R. D. Baker, G. L. Ebert, J. Hemmeter, A. J. Woldar. Maximal cliques in the Paley graph of square order. J. Statist. Plann. Inference 56 (1996) 33-38.

In the last century Geometry underwent several substantial extensions and revisions based on the fundamental revolutions that it lived through in the XIXth century.

The purpose of the lecture is to discuss several aspects of these transformations: the new concepts that emerged from these new points of view, the new perspectives that could be drawn, some bringing together the continuous and discrete viewpoints, some classical problems that could be solved, and the new interactions with other disciplines that went along.

The lecture is meant for a general mathematical audience.

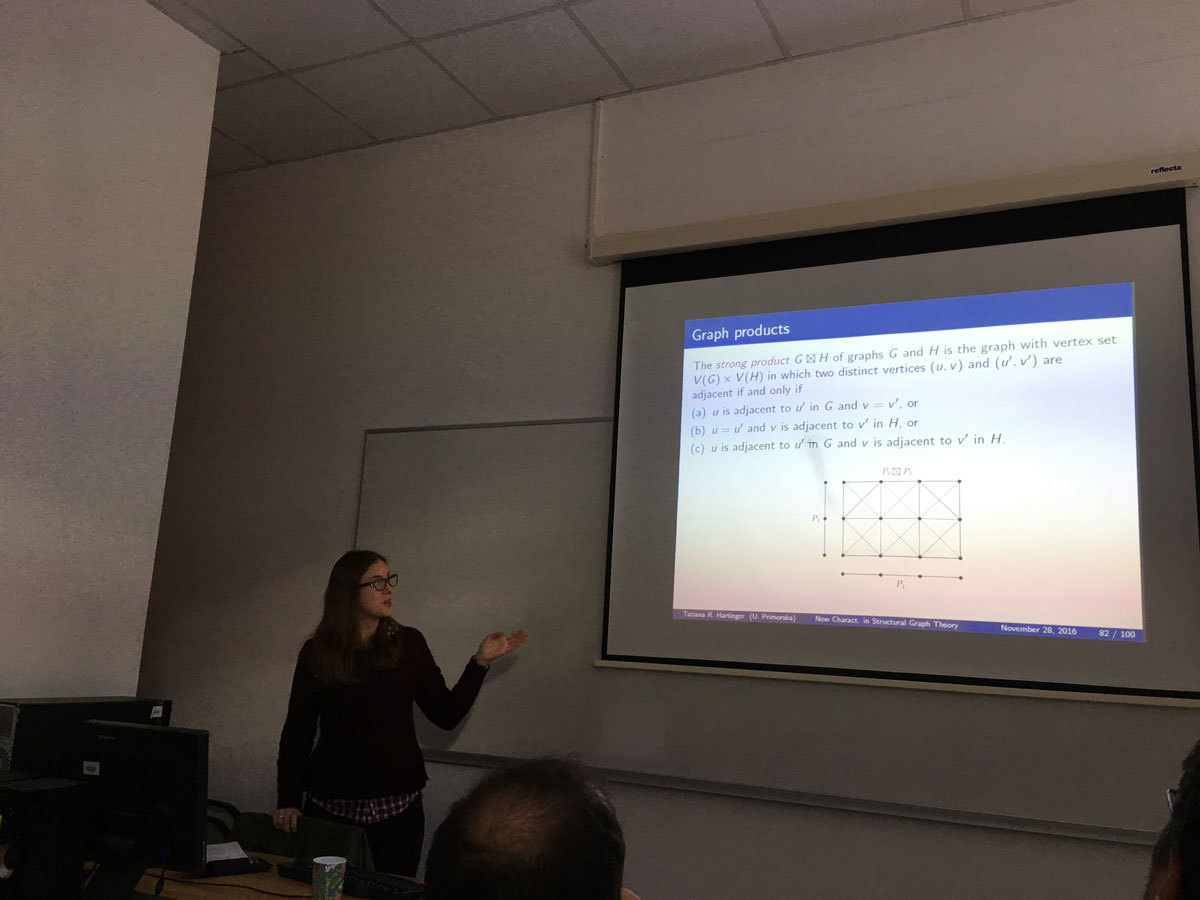
This is a presentation of PhD thesis topic. The PhD thesis will consist of three interrelated parts: 1-perfectly orientable graphs, graph products, and the price of connectivity. The central common theme among the three parts is the study of graph classes. In particular, we will examine three well known intersection graph classes which will play a key role in many of our results: chordal, interval, and circular arc graphs.

Following the terminology of Kammer and Tholey, we say that an orientation of a graph is 1-perfect if the out-neighborhood of every vertex induces a tournament, and that a graph is 1-perfectly orientable (1-p.o. for short) if it has a 1-perfect orientation. 1-perfectly orientable graphs are known to be polynomially recognizable, but a complete structural understanding of the class is still an open question. In the presentation we will discuss characterizations of 1-perfectly orientable graphs in various graph classes, including nontrivial product graphs for each of the four standard graph products (Cartesian, direct, strong, and lexicographic).

For a family of graphs F, an F-transversal of a graph G is a subset S in V(G) that intersects every subset of V(G) that induces a subgraph isomorphic to a graph in F. We denote by t_F(G) be the minimum size of an F-transversal of G, and by ct_F(G) be the minimum size of an F-transversal of G that induces a connected graph. For a class of connected graphs, we say that the price of connectivity of F-transversals is multiplicative if, for all G in the class, ct_F(G)/t_F(G) is bounded by a constant, and additive if ct_F(G)-t_F(G) is bounded by a constant. The price of connectivity is identical if t_F(G) and ct_F(G) are always equal and unbounded if ct_F(G) cannot be bounded in terms of t_F(G). The price of connectivity will be discussed in the context of hereditary graph classes defined by a single forbidden induced subgraph.

A graph G of even order is k-extendable if it has at least 2 k+2 vertices, contains a matching of size k, and if every k-matching is contained in a perfect matching of G. In the talk we will discuss 1-extendability and 2-extendability of Cartesian product of graphs and lexicographic products of graphs.

For a positive integer k, a graph is called a k-circulant if its automorphism group contains a cyclic semiregular subgroup with k orbits on the vertices. In this talk, I am going to discuss the following question: for which k there exist infinitely many cubic arc-transitive k-circulants? This is based on a joint work with Michael Giudici, Cai Heng Li and Gabriel Verret.

Abstract. A subgroup $H$ of a group $G$ is said to be pronormal in $G$ if $H$ and $H^g$ are conjugate in $\langle H, H^g \rangle$ for every $g \in G$. 
In this talk we will discuss a classification (in progress) of finite simple groups in which subgroups of odd indices are pronormal.

In its classical formulation Plateau problem asks to find the surface of minimal area spanning a given boundary. Understanding the proper notion of surface, area and of "spanning a  boundary" has lead since the pioneering works of Almegren-De Giorgi/Federe-Fleming/Reifenberg in the 50's to the development of beautiful and powerful tools in Geometric Measure Theory.

I will review the state of the art on the Plateau problem by presenting a series of old and new results concerning existence and regularity of solutions.

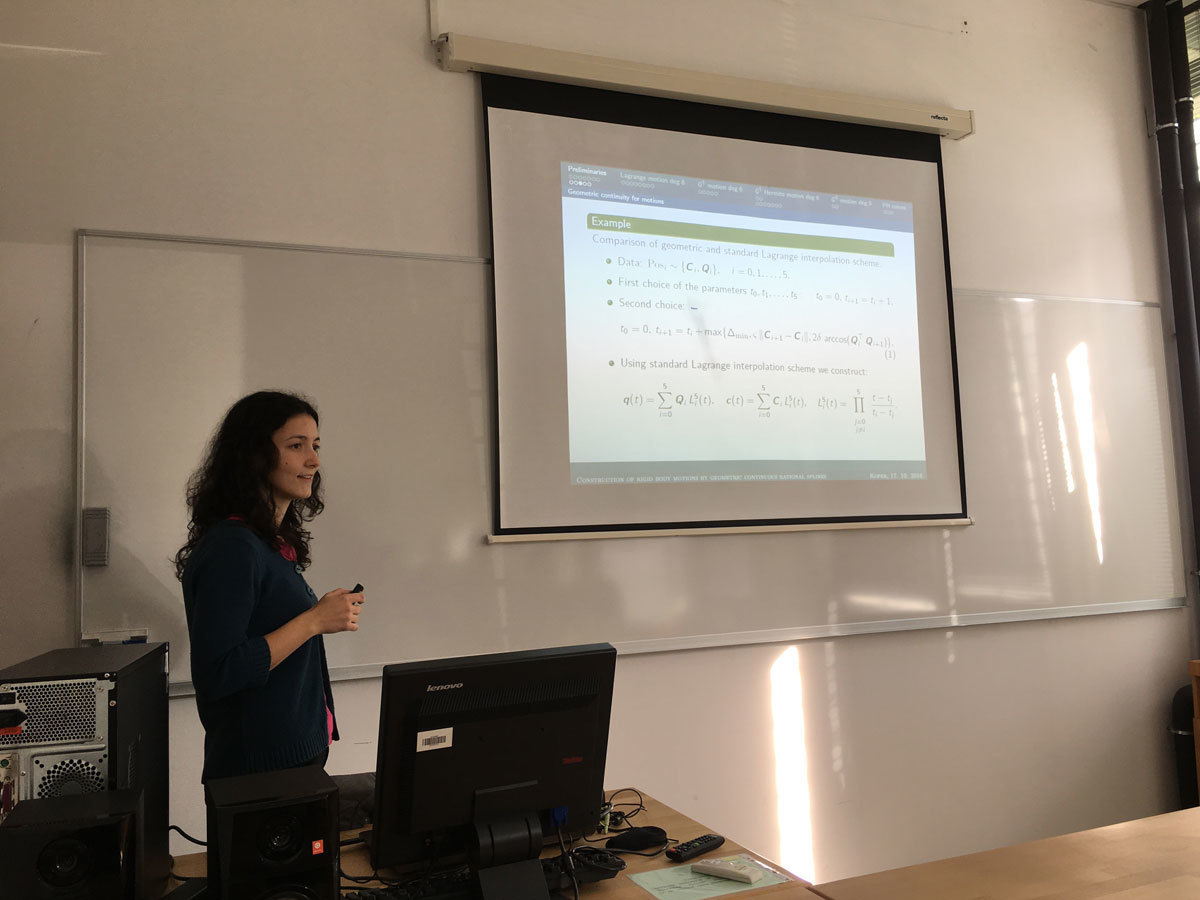
In this talk we present a geometric approach to interpolate given sequence of rigid body positions (i.e. center positions and orientations), which, in contrast to standard approaches, is free of choosing parameter values in advance and it enables the lowest possible degree of the motion. We introduce some interpolation problems and develop interpolation schemes for the construction of rigid body motions by rational splines of a low degree. A slightly different approach to motion construction, namely motion design with Euler-Rodrigues frames of Pythagorean-hodograph curves is also discussed. Two presented schemes for motions of degree three and five  are particularly useful in the applications, where the orientational component is not precisely specified and an algorithm must be formulated to determine a "natural" variation of orientation along the center trajectory. The theoretical results are substantiated with numerical examples.

We prove several generalizations of ramarkable Pascal's theorem which states that if we draw a hexagon inscribed in a conic section then the three pairs of opposite sides of the hexagon intersect at three points which lie on a straight line - the Pascal line of the hexagon. The complete figure formed by 60 Pascal's line has amazing properties ant it is known as Hexagrammum Mysticum. The similar results about an octagon inscribed in a conic section are known as Octagrammum Mysticum. We present an elementary combinatorial proof of those classical using Bézout’s theorem as the main tool whose application is guided by the empirical evidence and computer experiments with the program Cinderella.

The motivation for our research problem comes from hedging reserves in life insurance policies with guarantees. Since some supervisory authority advise to take a hedging strategy, where the number of units of a risky asset is determined to always be one, one should consider if there is some other hedging strategy, which would be at some point better to use. If there is such, when would be the optimal time to switch from one to another? We will look at some simulations that confirms our assumption of existing such hedging strategy and we will look when would be optimal to switch in a general mathematical case. This is joint work with Mihael Perman.

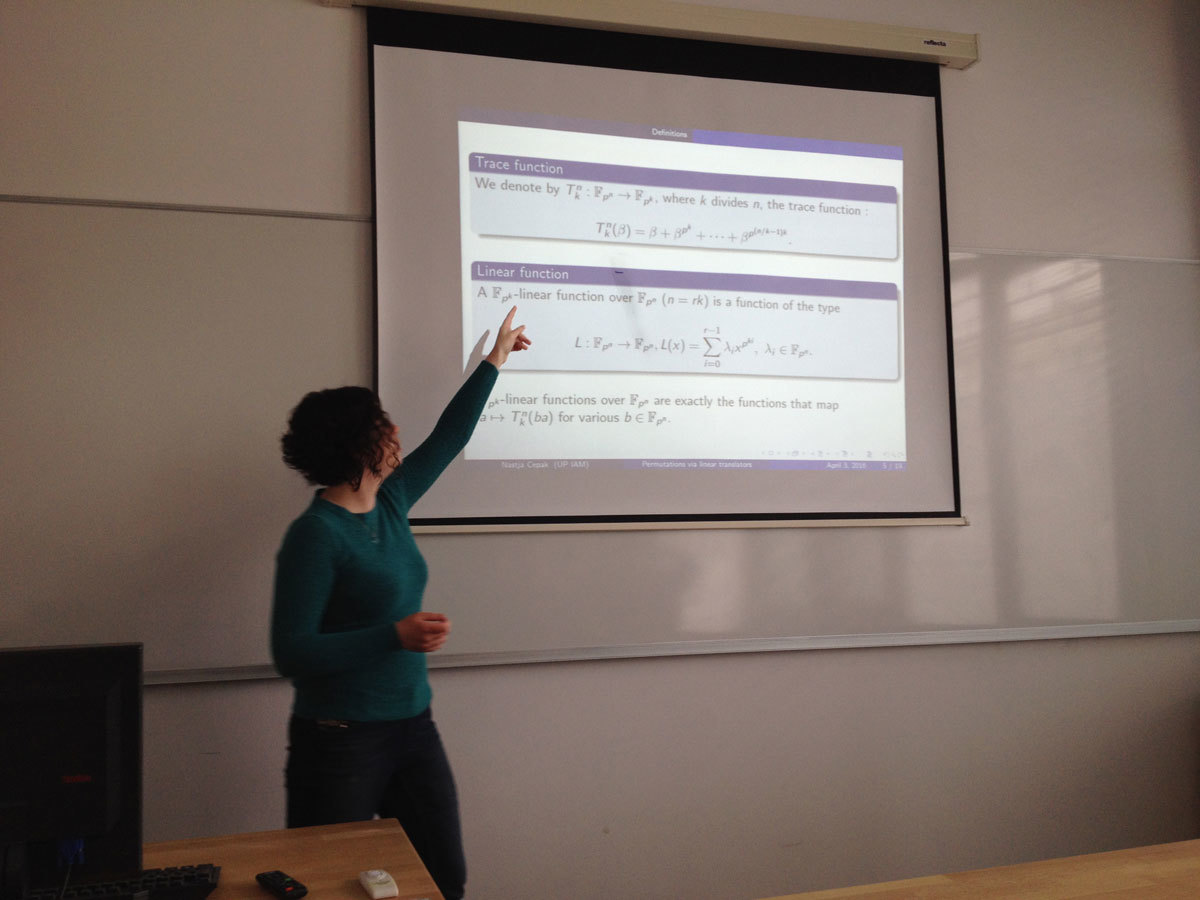
In difference to many recent articles that deal with generalized bent (gbent) functions $f:\mathbb{Z}_2^n \rightarrow \mathbb{Z}_q$ for certain small valued $q\in \{4,8,16 \}$, we give a complete description of these functions for both $n$ even and odd and for any $q=2^k$ in terms of both the necessary and sufficient conditions their component functions need to satisfy. This enables us to completely characterize gbent functions as algebraic objects, namely as affine spaces of bent or semi-bent functions with interesting additional properties, which we in detail describe. We also specify the dual and the Gray image of gbent functions for $q=2^k$. We discuss the subclass of gbent functions which corresponds to relative difference sets, which we call $\Z_q$-bent functions, and point out that they correspond to a class of vectorial bent functions. The property of being $\mathbb{Z}_q$-bent is much stronger than the standard concept of a gbent function.

In 1933 S. Ulam posed and K. Borsuk showed that if $n>m$ \newline then {\bf{it is impossible}} to map $f: S^n \to S^m$

\centerline{preserving symmetry: $f(-x)= -f(x)$ .}

Next in 1954-55, C. T. Yang, and D. Bourgin, showed that if $f: \mathbb{S}^n\to \mathbb{R}^{m+1}$ preserves this symmetry then

\centerline{$ \dim f^{-1}(0) \geq n-m-1$.}

We will present versions of the latter for some other groups of symmetries and also discuss the case $n=\infty$

Let $V$ and $W$ be orthogonal representations of a compact Lie group $G$ with $V^G = W^G=\{0\}$. 

Let $S(V )$ be the sphere of $V$ and $f:S(V ) \to W$ be a $G$-equivariant mapping.

We estimate the dimension of set $Z_f=f^{-1}\{0\}$ in terms of $ \dim V$ and $\dim W$, if $G$ is the torus $\mathbb T^k$, the $p$-torus $\mathbb Z_p^k$, or the cyclic group $\mathbb Z_{p^k}$, $p$-prime.

Finally, we show that for any $p$-toral group: $\;e\hookrightarrow \mathbb{T}^k \hookrightarrow G \to \mathcal{P}\to e$, $P$ a finite $p$-group and a $G$-map $f:S(V) \to W$, with $\dim V=\infty$ and $\dim W<\infty$, we have $\dim Z_f= \infty$

Bourgin-Yang_Primorska.pdf

The domination game is played on a graph $G$ by two players, Dominator and Staller. They are alternating turns in choosing vertices, one at a time, so that each chosen vertex enlarges the set of vertices of $G$ dominated to that point in the game. The game ends when all vertices of $G$ are dominated. The aim of Dominator is that the game ends in as few moves as possible, while Staller's goal is to maximize the number of moves. Assuming that both players play optimally, and that Dominator starts the game, the number of vertices chosen in the game is called the game domination number, $gamma_g(G)$; if Staller starts the game, we denote the resulting number of moves by $gamma_g'(G)$.

The domination game was introduced in 2010, and received a considerable attention by several authors. In this talk, I intend to give a brief overview of the results and methods related to the domination game. In particular, $3/5$-conjectures, relations between both versions of the game, and complexity issues will be presented.

In the attempt of solving the isoperimetric problem in 1838 Steiner missed the important point of the existence of the solution. Various authors found alternative proofs or filled the gap. W. Gross belongs to the second group (1917). He constructed, given a convex body K, a sequence of directions {u_n} such that iterated Steiner symmetrals taken in that directions minimize the perimeter and converge, in the Hausdorff distance, to the ball K^* centered at the origin and having the same volume as K.

Peter Mani (1986) was the first to understand that the convergence of iterated Steiner symmetrizations of a convex body K to K^* holds almost surely and conjectured that this happens also if we consider successive Steiner symmetrizations of a compact set. The conjecture was confirmed in 2006 by van Schaftingen. I provided in 2013 a different proof.

I conjectured in 2009 that density alone of the sequence {u_n} is sufficient for the convergence of the iterated Steiner symmetrization. P. Gronchi disproved the conjecture in 2010.

Bianchi, Klain, Lutwak, Yang and Zhang (2011) proved however the following result:

Theorem. If K is a convex body and U is a countable and dense set of directions, then it can be ordered in a sequence {u_n} such that the successive Steiner iterations of K in that directions converge in the Hausdorff metric to the ball K^*.

I improved recently this result in two directions (2015, visible on line). On one hand the seed K of the iteration is allowed to be compact rather than just convex, and moreover there exists a universal ordering of U which works for every seed.

In the talk we will describe the recent result of the speaker how to construct a holomorphic function on the open unit ball B_N of C^N, N>1, whose real part is unbounded on every path in B_N of finite length that ends on bB_N. Level sets of such functions are examples of complete complex hypersurfaces in the ball and give a complete answer to a question of P. Yang from 1977 about the existence of bounded complete complex manifods. We will also present a generalization of this result to pseudoconvex domains in C^N and a related result obtained jointly with A. Alarcon and F. J. Lopez about a construction of a complete proper holomorphic embedding from the open unit disc in C to B_2.

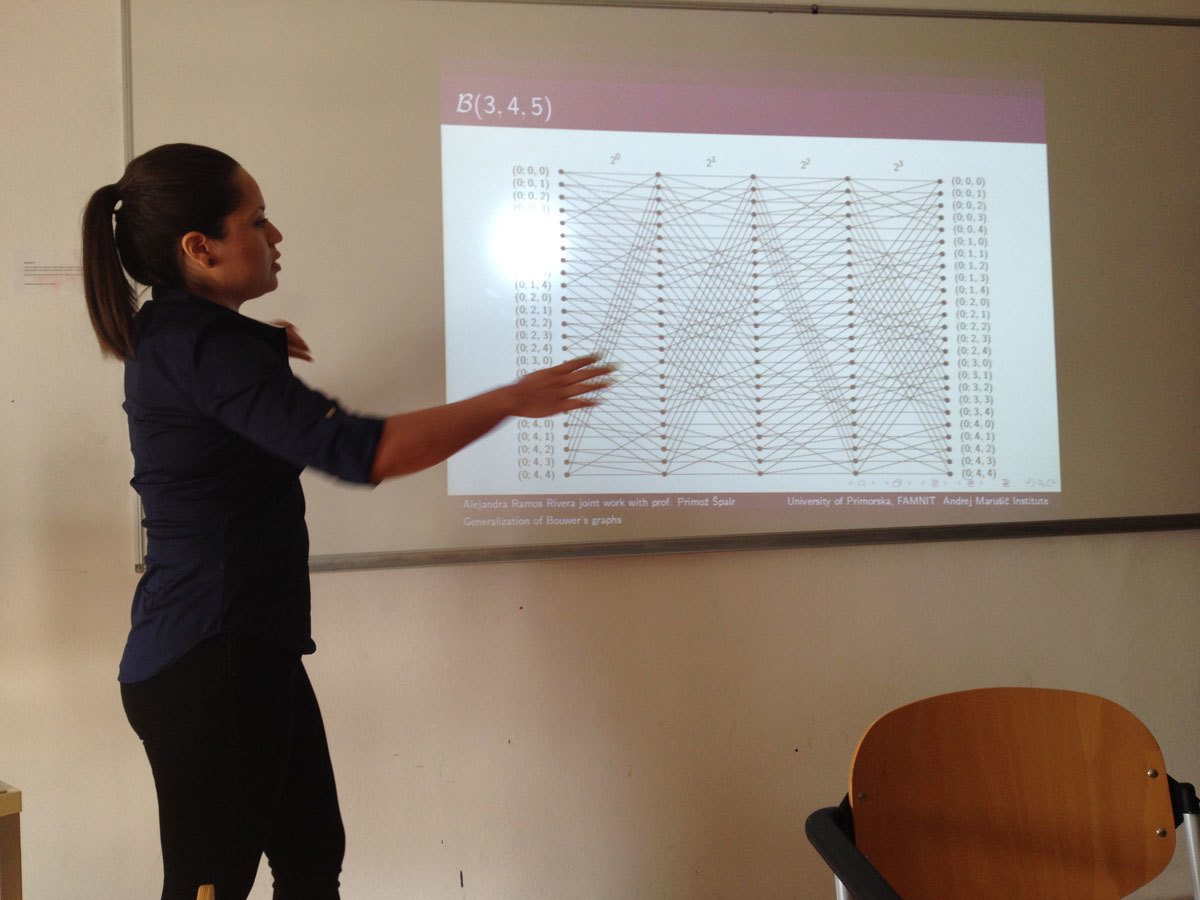
Bouwer proved that there exists a half-transitive graph of every even valency greater that 2, by giving a contruction for a family of graphs now known as B(k,m,n). Recently, it was proved by M. Conder and A. Žitnik which of Bower’s graphs are half-arc-transitive.

Let D_G(X) be one of the two opposedly oriented digraphs associated with a half-transitive graph X with respect to the action of Aut(X). Two arcs are related if they have the same initial vertex (tail), or the same terminal vertex (head). The subgraphs consisting of equivalence classes of directed edges of this relation are called alternets.

Let {\cal A} = {A_i | i\in {1, 2, ... ,m}} be the set of alternets in X and for each i\in {1, 2, . . . ,m} define H_i to be the set of all vertices at the heads of arcs in A_i\in{\cal A}, and T_i be the set of all vertices at the tail of arcs in A_i. If H_i = T_j for some i, j\in {1, 2, ... ,m}, then X is said to be tightly attached. Tightly attached graphs with valency 4 were classified by P. Šparl and D. Marušič.

In this talk a family of tightly attached half-transitive graphs with valency 2k is introduced as a generalization of the Bouwer’s graphs. 

Based on joint work with Primož Šparl.

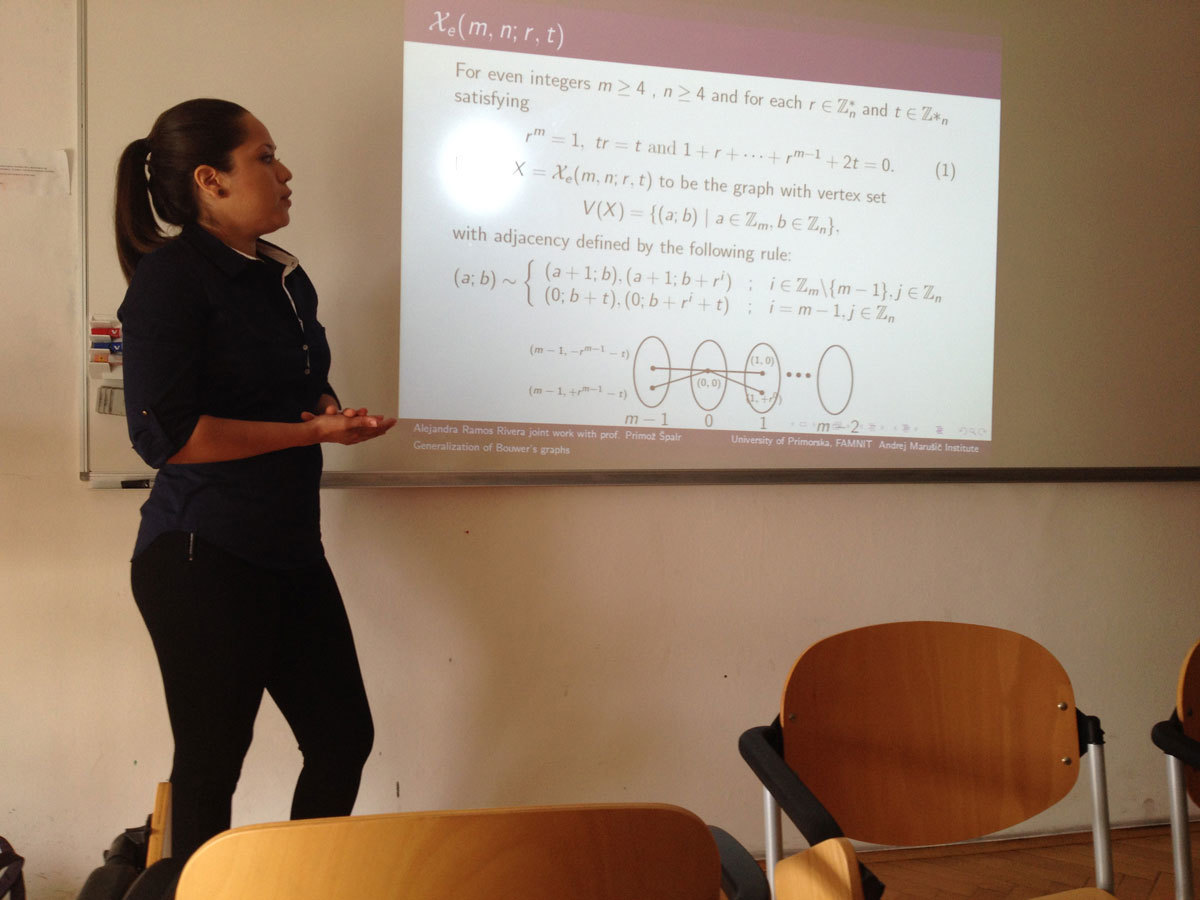
This talk gives a survey on the state of the art in the classification of the finite groups of prime-power order. Given a prime p and a natural number n, one can consider the function f(p,n) of groups of order p^n (up to isomorphism). The function f(p,n) can be considered as a function in p or as a function in n and then has different interesting asymptotic properties. However, using the order is not the only way to approach the classification of groups of prime-power order. An alternative approach is to classify the groups of prime-power order using their coclass as primary invariant. The talk will explain this in more detail and also exhibit some of the results of this approach.

We consider the problem of finding the smallest vertex-transitive k-regular graphs of girth g. Counting cycles and using number theory's theorems we extend Biggs's result proving that the asymptotic density of the set of all odd girths g for which exists a vertex-transitive (k,g)-cage with excess not exceeding e is 0. Also, we consider the existence of (k,g)-vertex-transitive graphs when g is even and the excess is 4 or smaller than min{k-2,g}.

Based on joint work with Robert Jajcay.

The family of generalized Petersen graphs G(n,k), introduced by Coxter et al. (1950) and named by Mark Watkins (1969), is a family of cubic graphs formed by connecting the vertices of a regular polygon to the corresponding vertices of a star polygon. The Kronecker cover of a simple undirected graph G  is a a special type of bipartite covering graph of G, isomorphic to the direct (tensor) product of G and K_{2}. In the seminar we will identify generalized Petersen graphs G(n,k) that are Kronecker covers of another generalized Petersen graphs, and discuss some related questions.

We show that many infinite classes of permutations over finite fields can be constructed via translators with a large choice of parameters. We characterize some functions having linear translators, based on which several families of permutations are then derived. We give in several cases the compositional inverse of these permutations. The connection with complete permutations is also utilized to provide further infinite classes of permutations.

In this talk we'll describe some properties of certain discrete subgroups of quaternionic matrices acting in the hyperbolic quaternionic space which are similar to the modular group in the complex case: we highlight similarities and differences. This work is in collaboration with J.P Diaz Gonzalez and A. Verjovsky (UNAM Cuernavaca, Mexico)

We study codes spanned by the rows of an orbit matrix of a symmetric design with respect to an automorphism group that acts with all orbits of the same length. The dimension of such codes is discussed. We define an extended orbit matrix and show that under some condition the rows of the extended orbit matrix span a code that is self-dual with respect to a certain scalar product.

Based on joint work with Dean Crnković.

A graph G is said to be 1-perfectly orientable (1-p.o. for short) if it admits an orientation such that the out-neighborhood of every vertex is a clique in G. The class of 1-p.o. graphs forms a common generalization of the classes of chordal and circular arc graphs. Even though 1-p.o. graphs can be recognized in polynomial time, no structural characterization of 1-p.o. graphs is known. In this paper we consider the four standard graph products: the Cartesian product, the strong product, the direct product, and the lexicographic product. For each of them, we characterize when a nontrivial product of two graphs is 1-p.o.

Based on joint work with Martin Milanič.

Let \Gamma denote a bipartite distance-regular graph with diameter D \ge 4 and valency k \ge 4. Let X denote the vertex set of \Gamma, and let A denote the adjacency matrix of \Gamma. For x \in X and for 0 \le i \le D, let \G_i(x) denote the set of vertices in X that are distance i from vertex x. Define a parameter \Delta_2 in terms of the intersection numbers by \Delta_2 = (k-2)(c_3-1)-(c_2-1)p^2_{22}. It is known that \Delta_2 = 0 implies that D \le 5 or c_2 \in \{1,2\}. 

For x \in X let T=T(x) denote the subalgebra of \Mat_X(\C) generated by A, \Es_0, \Es_1, ..., \Es_D, where for 0 \le i \le D, \Es_i represents the projection onto the i-th subconstituent of \Gamma with respect to x. We refer to T as the Terwilliger algebra of \Gamma with respect to x. By the endpoint of an irreducible T-module W we mean min\{i | \Es_iW \ne 0\}.  

Building on the work of [MacLean, Miklavič and Penjić: On the Terwilliger algebra of bipartite distance-regular graphs with \Delta_2=0 and c_2=1, Linear Algebra and its Applications 496 (2016)] we find the structure of nonthin irreducible T-modules of endpoint 2 for graphs \Gamma in which for 2\le i\le D-1 there exist complex scalars \alpha_i, \beta_i with the following property: for all x, y, z \in X such that \partial(x, y) = 2, \partial(x, z) = i,  \partial(y, z) = i we have \alpha_i + \beta_i  |\G_1(x) \cap \G_1(y) \cap \G_{i-1}(z)| = |\G_{i-1}(x) \cap \G_{i-1}(y) \cap \G_1(z)|; in case when \Delta_2=0 and c_2=2.

We show that if \Gamma is not almost 2-homogeneous, then up to isomorphism there exists exactly one irreducible T-module with endpoint 2 and it is not thin. We give an basis for this T-module, and we give the action of A on this basis. The isomorphism class of such a given module is determined by the intersection numbers of the \Gamma. 

DiscreteZOO is a project combining a central repository of graphs, its website front-end and extensions for software packages like Sage. The repository contains certain precomputed properties to speed up the processes of filtering, searching and computation. For now it can store graphs, with the groundwork already laid out for more combinatorial objects (such as maps, maniplexes, geometries, etc.).

In the talk we will show how one can interact with DiscreteZOO on the example of the censuses of vertex transitive graphs by Royle, Conder, and Potočnik, Spiga and Verret. We will perform some example searches on the website, download a subset of the database and showcase some queries that can be run locally with the Sage package.

We will present solutions to several problems published in recent volume of ILAS publication IMAGE. Problems are intended to popularize the field of Linear algebra.

http://www.ilasic.org/IMAGE/

In the past we have been using flag graphs and symmetry type graphs for studying certain operations on maps and their symmetries, such as truncation, dual, medial, chamfering, etc. Here we study similar operations on oriented maps. Certain new operations that can only be defined for oriented maps, such as snub, are considered. In the oriented case the primary tools, i.e. flag graphs and symmetry type graphs, are substituted by arc graphs and oriented symmetry type graphs. Same ideas apply to operations on maniplexes and oriented maniplexes and henceforth to polytopes and oriented polytopes. In particular, it is shown that the "twist" operation that Steve Wilson introduced in his talk in Veszprem is naturally defined on oriented maniplexes rather than orientable ones. The talk will be presented using Sage. This is work in progress with Leah Berman,  Gordon Williams and Steve Wilson.

The objective of this talk is to provide an introduction to several open problems about the monodromy groups of abstract polytopes and how they relate to the study of coverings of abstract polytopes by regular abstract polytopes.

Abstract polytopes are a generalization of convex polytopes to purely combinatorial objects, as partially ordered sets satisfying some relatively straightforward constraints. The most symmetric type of abstract polytopes, the regular abstract polytopes, have been studied extensively, and their analysis has been greatly facilitated by the study of their automorphism groups. However, non-regular abstract polytopes are poorly understood, in part because their automorphism group doesn't give enough information about their structure. To begin to investigate non-regular polytopes, we have used two main tools: representation of non-regular polytopes as quotients of regular polytopes, and analysis of the "monodromy group" of the polytope, which encodes combinatorially the connective structure of the polytope. There are important relationships between these two representations, and understanding the relationship motivates many interesting problems in the theory of non-regular abstract polytopes.

This talk will assume no background understanding of either abstract polytopes or monodromy groups. I will provide basic definitions and examples to illustrate both important basic facts about what we have learned about quotient representations and monodromy groups, as well as facilitate introducing open problems in the area.