Raziskovalni matematični seminar - Arhiv

In this talk, we will revisit the variety of antilattices and its connection with magic squares. This is work in progress with Karin Cvetko-Vah.

In matching theory it is a basic problem to determine all the edges in a given graph which can be extended to a maximum matching. Such edges are called maximally-matchable or allowed edges. In addition to its theoretical relevance this question has application in anonymity problems in databases and certain propagation methods in constraint programming. In the last years researchers from graph theory as well as from the above applications fields developed efficient polynomial time algorithms for the identification of allowed edges, but from practicalpo int of view only the bipartite solution is satisfactory for larger scale problems. While the bipartite case can be easily solved in linear time with respect to the number of edges, the complexity gap with the nonbipartite case is significant: a magnitude of the number of vertices.

In this talk first we will review the methods from the literature for determining the maximally-matchable edges. Then a decomposition theory based on the matching structure is presented with showing the related algorithmic concept for identifying the allowed edges. Finally we will show that a fixed-parameter linear time divide-and-conquer algorithm can be worked out for non-bipartite graphs, where the complexity of the new method will be expressed with the help of a graph parameter arising from the developed decomposition structure.

The talk is based on a joint work with Radoslaw Cymer (Augsburg).

The notion of density of a subgraph is usually defined as the number of edges in the subgraph divided by the number of its vertices. However, this definition is too permissive for the characterization of communities in graphs where each vertex should be densely connected within the community, with regard to its degree. Motivated by the idea of defining a notion of density more suitable for the study and identification of communities in graphs, we will be interested in the property of "proportional density". Specifically, we define a "proportionally dense subgraph" (PDS) as an induced subgraph such that each vertex in the PDS has proportionally more neighbors inside the PDS than in the whole graph. We will focus on the problem of finding a PDS of maximum size. Some hardness results on restricted classes of graphs will be presented (NP-hardness and APX-hardness), as well as a very simple polynomial-time 2-approximation algorithm. In the last part of the talk, we will give an upper bound on the size of a PDS in a graph based on its maximum degree and prove that all Hamiltonian cubic graphs have a PDS that reaches this bound.

Axial algebras are non-associative algebras generated by semisimple idempotents, known as axes, whose eigenvectors obey a given fusion law. These algebras have been shown to occur in many areas of mathematics but are of particular interest thanks to their rich relationship to certain groups. Dihedral axial algebras are those generated by two axes and are fundamental to the study of axial algebras in general. We present a new result that classifies in high generality dihedral axial algebra whose fusion laws have three or fewer eigenvalues. This result represents a significant broadening of our understanding of axial algebras.
 

Given a graph X and a group G we may construct a covering graph Cov(X,Z) by means of a function (called a voltage assignment) Z, that maps arcs of the graph X to elements of the group G. The graph Cov(X,Z) is called the regular cover of X arising from the voltage graph (X,Z) and admits a semiregular (fixed point free) group of automorphisms isomorphic to G. Every graph X with a semiregular group of automorphism G can be regarded as the regular cover of the quotient graph X/G with an appropriate voltage assignment. The theory of voltage graphs and their associated regular covers has become an important tool in the study of symmetries of graphs. We present a generalised theory of voltage graphs where G is allowed to be an arbitrary group (not necesarilly semiregular).

Axial algebras are a recently defined type of nonassociative algebras. They are primarily used to realize groups inside the automorphism group of such an algebra. The prominent example is the Griess algebra that was used in 1982 by R.L. Griess to construct the largest sporadic simple group known as the Monster group. Recently, various other groups were realized in this fashion.

In this project, we have introduced modules over axial algebras. If an axial algebra gives rise to a certain group, then the modules of this algebra naturally correspond to representations of (a central extension of) this group.

We will explain the definitions, give examples and provide some insight into recent developments. We will illustrate how the connection between axial algebras and groups can help us to get a better understanding of both. Joint work with Tom De Medts.

Matroids are combinatorial objects designed to capture essential features of the notion of (linear) independence. They show up naturally in several contexts, including algebraic geometry, topology and optimisation. We will introduce an invariant of matroids called the h-vector that arises when studying the matroid in algebraic and topological contexts. We will explain an old conjecture of Stanley about these h-vectors, survey what is known and explain a new connection with discrete geometry. We will not assume previous knowledge of matroid theory.

A bipartite biregular (n,m;g)-graph G is a bipartite graph of even girth g having the degree set {n,m} and satisfying the additional property that the vertices in the same partite set have the same degree.
An  (n,m;g)-bipartite biregular cage is a bipartite biregular (n,m;g)-graph of minimum order. In our talk, we present lower bounds on the orders of bipartite biregular (n,m;g)-graphs, and call the graphs that attain these bounds bipartite biregular Moore cages.

In parallel with the well-known classical results relating the existence of k-regular Moore graphs of even girths g = 6,8 and 12 to the existence of projective planes, generalized quadrangles, and generalized hexagons, we prove that the existence of S(2,k,v)-Steiner systems  yields the existence of  bipartite biregular (k,\frac{v-1}{k-1};6)-Moore cages. Moreover, in the special case of Steiner triple systems (i.e., in the case k=3), we completely solve the problem of the existence of (3,m;6)-bipartite biregular cages for all integers m greater or equal than 4. Considering girths higher than 6 and prime powers s, we relate the existence of generalized polygons (quadrangles, hexagons and octagons) with the existence of (n+1,n^2+1;8), (n+1,n^3+1;12), and (n+1,n^2+1;16)-bipartite
biregular Moore cages, respectively. Using this connection, we derive improved upper bounds for the orders of bipartite biregular cages of girths 8, 12 and 14.

This is joint work with Alejandra Ramos Rivera, Slobodan Filipovski and Gabriela Araujo Pardo.

Given a graph G, a minimal separator in G is a subset of vertices that separates some non-adjacent vertex pair a, b and is inclusion-minimal with respect to this property (separation of a and b). Minimal separators in graphs are an important concept in algorithmic graph theory. In particular, many problems that are NP-hard for general graphs are known to become polynomial-time solvable for classes of graphs with a polynomially bounded number of minimal separators. Graph classes having polynomially bounded number of minimal separators are called tame. Several well-known graph classes are tame, including chordal graphs, permutation graphs, circular-arc graphs, and circle graphs. We perform a systematic study of the question which classes of graphs defined by small forbidden induced subgraphs are tame. We focus on sets of forbidden induced subgraphs with at most four vertices and obtain a complete dichotomy.

Joint work with Martin Milanič.

It is known that a Cayley digraph Cay(A, S) of an abelian group A is isomorphic to a nontrivial wreath product if and only if there is a proper nontrivial subgroup B≤A such that S\B is a union of cosets of B in A. We generalize this result to Cayley graphs Cay(G, S) of nonabelian groups G by showing that such a digraph is isomorphic to a nontrivial wreath product if and only if there is a proper nontrivial subgroup H≤G such that S\H is a union of double cosets of H in G. This result is proven in the more general situation of a coset digraph. We will also discuss implications of this result to coset digraphs. This is joint work with Rachel Barber of Mississippi State University.

11:15 – 12:00: FAMNIT-VP1

Lecturer: Martin R Bridson FRS, 8ECM Prize Committee Chair (University of Oxford)

Title: Hyperbolic geometry: where battered gems retain their full beauty

Abstract: Hyperbolic geometry provides a rich setting in which many rigidity phenomena emerge. In this talk for a general audience, I shall present several different types of rigidity phenomena, from Mostow’s classical rigidity theorem to generalizations involving the large-scale geometry of groups and spaces. I shall also explain why hyperbolicity is so ubiquitous. I shall end by sketching how a newly discovered rigidity phenomenon in hyperbolic geometry can be used to settle an old question concerning the difficulty of identifying an infinite group by studying its actions on finite objects.

12:00 – 12:45: FAMNIT-VP1

Lecturer: Maria J. Esteban, 8ECM Scientific Committee Chair (CEREMADE (CNRS UMR n° 7534), PSL Research University, Université Paris-Dauphine)

Title: Best constants for functional inequalities and spectral estimates for Schrödinger operators

12:45 – 13.30: Lunch Break (Catering)

13:30 – 14.15: FAMNIT-VP1

Lecturer: Volker Mehrmann, President, European Mathematical Society (TU Berlin)

Title: The distance to stability and the distance to instability of dynamical systems

Abstract: The analysis of the stability of a dynamical system is an essential question of mathematics. An important class of control systems is that of dissipative Hamiltonian systems that arise in all areas of science and engineering. When the system is linearized around a stationary solution one gets a linear dissipative Hamiltonian system. Despite the fact that the system looks very unstructured at first sight, it has remarkable properties. Stability and passivity are automatic, Jordan structures for purely imaginary eigenvalues, eigenvalues at infinity, and even singular blocks in the Kronecker canonical form are very restricted and furthermore the structure leads to fast and efficient iterative solution methods for associated linear systems. We discuss the distance to instability under structure preserving perturbations and also the smallest distance to the nearest stable system. An even harder problem is the distance to the nearest singular or ill-posed problem. While this in general open, for the class of dissipative Hamiltonian systems we present a simple classification. This is joint work with Christian Mehl and Michal Wojtylak.

A colouring of a graph G is called asymmetric if the identity is the only auto-morphism preserving the colouring. The distinguishing number D(G) of a graph G is the least number of colours in an asymmetric vertex colouring. It was introduced by Albertson and Collins in [1], and was first considered for infinite graphs by Imrich, Klavžar and Trofimov in [3]. Asymmetric edge colourings were first investigated by Kalinowski and Pilśniak in [4], and for infinite graphs by Broere and Pilśniak [2]. In the talk, we survey results on asymmetric vertex and edge colourings of infinite graphs. We give known general upper bounds in terms of maximum degree. We focus mainly on several classes of graphs which need only two or three colours to break all nontrivial automorphisms. The most intriguing conjecture in this area is the Infinite Motion Conjecture posed by Thomas Tucker that every connected locally finite graph, such that every nontrivial automorphism moves infinitely many vertices, has the distinguishing number at most two. We show some very recent results obtained together with Lehner and Stawiski in this topic.

[1] M.O. Albertson, K. L. Collins, Symmetry breaking in graphs, Electron. J. Combin. 3 (1996), R18.

[2] I. Broere, M. Pilśniak, The Distinguishing Index of the Infinite Graphs, Electron. J. Combin. 23 (2015), P1.78.

[3] W. Imrich, S. Klavžar, V. Trofimov, Distinguishing infinite graphs, Electron. J. Combin. 14 (2007), R36.

[4] R. Kalinowski, M. Pilśniak, Distinguishing graphs by edge-colourings, European J. Combin. 45 (2015), 124–131.

In the talk, we will discuss edge-colorings of (sub)cubic graphs. Namely, we will consider edge-colorings in which we work with two types of colors: the proper and the strong colors. The edges colored with the same proper color form a matching (no two edges are incident), and the edges colored with the same strong color form an induced matching (no two edges are incident to a common edge). Clearly, when all the colors are proper, the edge-coloring of a graph is proper, and if all the colors are required to be strong, we have a strong edge-coloring. The tight upper bounds for the chromatic indices of the above two extremal colorings are long established, thus we will focus to edge-colorings with combinations of proper and strong colors. Such colorings have been investigated before, but only as a tool to obtain results for other types of colorings. Systematically, they have been introduced just recently by Gastineau and Togni as the edge coloring variation of S-packing colorings. We will present results on the topic and give a number of open problems.

In this talk we survey the results of our recent research on the 'symmetries' of different structures of positive (semi)definite matrices. In those results we give exact descriptions of certain algebraic endomorphisms/automorphisms (such as Jordan triple endomorphisms, sequential endomorphisms), isometries corresponding to different distances, and transformations preserving divergences (among others, different sorts of relative entropies).

Starting from 2017, several quasi-polynomial algorithms for solving parity games were suggested. Using universal ordered trees and automata separation approach gives a very natural quasi-polynomial algorithm for solving parity games. Moreover, many other algorithms can be expressed in terms of automata separation approach. In the talk the construction of near-optimal universal trees will be presented and the basics of automata separation approach for solving parity games will be discussed.

The talk is based on the work of Czerwinski, Daviaud, Fijalkow, Jurdzinski, Lazic and Parys.

About lecturer: https://www.hse.ru/en/org/persons/14007605

In my talk I will describe a construction, which answers the following question: given a triangulation of an oriented principal circle bundle P over a simplicial complex K (bundle projection is supposed to match the triangulations, i.e. it should be a simplicial map), find a  simplicial cochain in K, representing the Chern class of P. I will explain  the necessary definitions and if time permits describe briefly possible  generalizations of this construction. The talk is based on joint work with  N. Mnёv, POMI.

A simplicial complex is shellable if it exhibits a well-behaved ordering of its maximal faces (a shelling) constructed in some precise way.Shellings have been proven useful, but they are generally not easy to construct. It is natural to ask whether shellings may be efficiently found computationally. However, it was recently proved by Goaoc, Paták, Patáková, Tancer and Wagner that deciding whether a simplicial complex is shellable is an NP-complete problem. In this talk, we use a different approach (relative shellability) to sketch a new proof for NP-completeness of shellability.

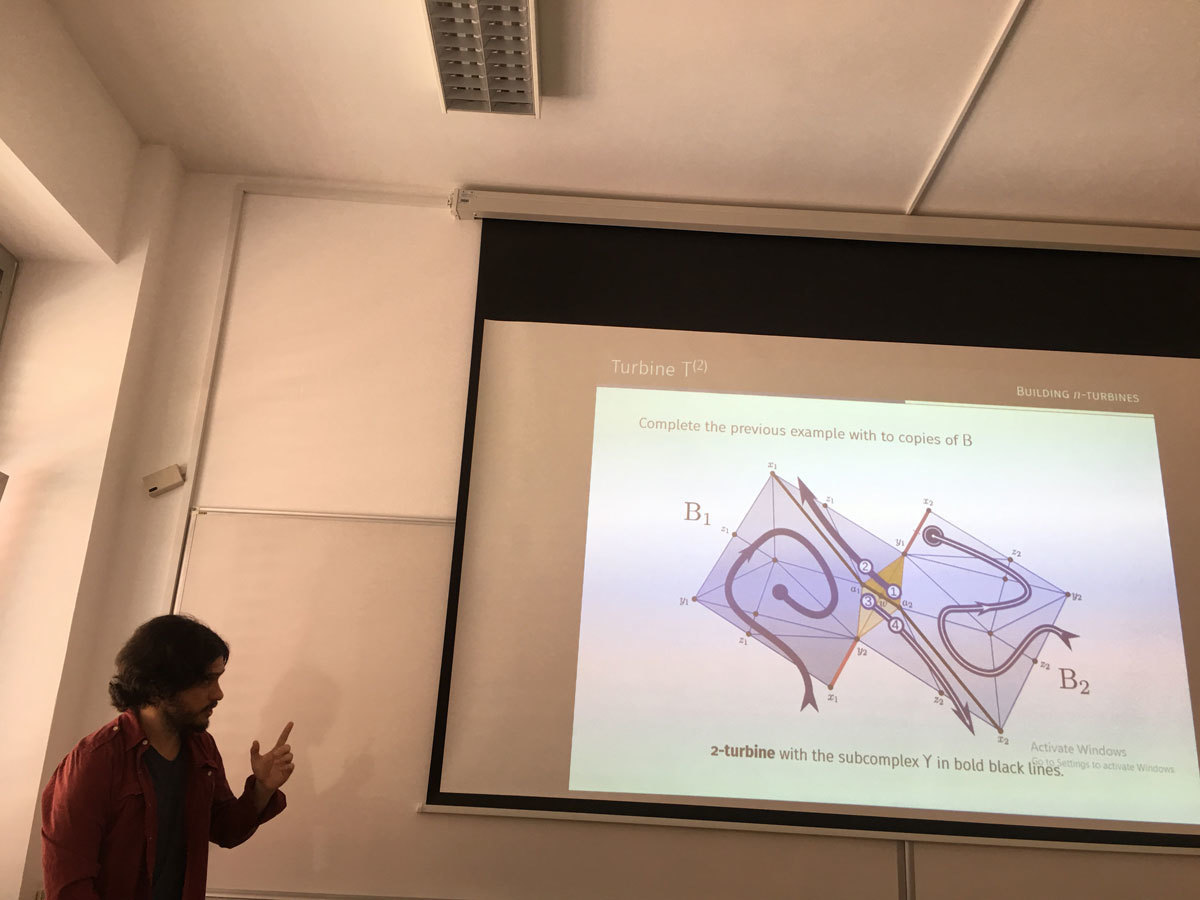
In this talk I cover the entire history of mathematics in one hour, from earliest times to the modern age, illustrating the narrative with about 300 attractive (and sometimes bizarre) postage stamps from around the world, featuring mathematics and mathematicians.

In the first part of this talk we introduce Game Theory, its solution concepts and applications. We then discuss the limits of classical game-theoretic predictions and give possible reasons for that. At the end of the first part we present some behavioral and evolutionary models. These models have better predictive power than classical models and are therefore more useful in real life.

In the second part of this talk a joint work with Assoc. Prof. A. Ule is presented. The main topics of our research are reputation and (dis)honesty.  Dishonesty has a negative impact on everyone if and when the truth is revealed, and the consequences can be severe. How dishonesty spreads through the social network? Can we eliminate (or at least reduce) harmful lies and mistrust, and thus inefficiency? We try to answer these kind of questions.

We are also interesting in finding stable strategies, i.e. strategies that persist over time. We present our theoretical model and (partial) results. In order to get some new insights about people behavior (e.g. what strategies do people use), we also ran a pilot experiment. The experimental results are presented in the last part of the talk.

Linear complementarity problems (LCP) generalizes some fundamental problems of mathematical optimization like linear programming (LP) problem, linearly constrained quadratic programming (LQP) problem and some other. It admits an enormous number of applications in economics, engineering, science and many other fields. After all these, it is not surprising that LCPs are usually NP-complete problems (S.J. Chung, 1989).

The three most significant classes of algorithms for solving LCP problems are: pivot algorithms (PA), interior point algorithms (IPA) and continuation methods. Because, both PA and IPA have been developed earlier for LP and QP problems it is quite natural idea to test them on LCP problems, as well.

Concept of sufficient matrices, as generalization of positive semidefinite matrices, has been introduced 30 years ago by Cottle et al. (1989). LCPs with sufficient matrices posses many important properties, like the solution set is convex and polyhedral; guarantees the finiteness of PAs and (pseudo) polynomial behaviour of the IPAs. 

The largest matrix class where the interior point algorithms (IPA) are polynomial is the class of P*(κ)-matrices, for given nonnegative real parameter κ. The union for all possible κ parameters of P*(κ)-matrices forms the class of P*-matrices. This class of matrices has been introduced by Kojima et al. in 1991. Known IPAs for LCPs with P*(κ)-matrices under the interior point assumption, possess polynomial iteration complexity depending on the problem size n, parameter κ and the bit length L of the rational data of the LCP.

After all of these, it is a natural question: What is the relation between the sufficient and P*-matrices? Väliaho (1996) proved that the P*-matrices are exactly those which are sufficient. Unfortunately, there are two important, negative results related to sufficient matrices. P. Tseng (2000) proved that decision problem related to the membership of matrices for P0- and column sufficient matrices are all co-NP-complete. While de Klerk and Eisenberg-Nagy showed that there exists such P*(κ)-matrices for which the κ value is exponential in the size n of the problem.

Furthermore, for sufficient LCPs, it is meaningful to introduce dual LCP problem and it can be proved that from sufficient primal- and dual LCP problem, exactly one has solution, that is an interesting, nice and (quite) new generalization of the old Farkas’ lemma.

There are still several open questions in the area of sufficient LCPs. More importantly, solution methods developed for sufficient LCPs helps us in trying to solve LCP problems with more general matrices.

e-mail: illes@math.bme.hu
homepage: https://det.math.bme.hu/illes-tibor

Given a code in a graph, the vertex set of the graph may be partitioned by the sets of vertices at each of the possible distances to the code. If the automorphism group of the code acts transitively on each cell of this `distance partition', then the code is called `completely transitive'. I will discuss recent work towards a classification of binary completely transitive codes, and briefly discuss related algebraic and combinatorial symmetry conditions.

A connected dominating set in a graph is a dominating set of vertices that induces a connected subgraph. In this talk we present graphs in which connected dominating sets can be separated from the other vertex subsets by a linear weight function. More precisely, we say that a graph is connected-domishold if it admits non-negative real weights associated to its vertices such that a set of vertices is a connected dominating set if and only if the sum of the corresponding weights exceeds a certain threshold. We characterize the graphs in this non-hereditary class in terms of a property of the set of minimal cutsets of the graph, and we also give several characterizations for the hereditary case, that is, when each connected induced subgraph is required to be connected-domishold.

We construct new explicit vacuum solutions of quadratic metric-affine gravity. The approach of metric-affine gravity in using an independent affine connection produces a theory with 10+64 unknowns, which implies admitting torsion and possible nonmetricity. Our spacetimes are generalisations of classical pp-waves, four-dimensional Lorentzian spacetimes which admit a nonvanishing parallel spinor field. We generalize this definition to metric compatible spacetimes with pp-metric and purely axial torsion. It has been suggested that one can interpret that the axial component of torsion as the Hodge dual of the electromagnetic vector potential. We compare these solutions with our previous results and other solutions of classical models describing the interaction of gravitational and neutrino fields.

Hypergraphs are generalizations of graphs in which edges (in this context referred to as hyperedges) can have arbitrary cardinality. A hypergraph is Sperner if no hyperedge contains another one. A Sperner hypergraph is equilizable if the characteristic vectors of its hyperedges are the binary solutions to a linear equation with positive coefficients. Threshold (Sperner) hypergraphs are defined similarly, with respect to minimal binary solutions of a linear inequality with positive coefficients. These combinatorial notions have many applications and are motivated by the theory of Boolean functions and integer programming. We introduce the class of 1-Sperner hypergraphs, defined by the property that for every two hyperedges the smallest of their two set differences is of size one. We characterize this class of Sperner hypergraphs by a decomposition theorem and derive several consequences from it, including bounds on the size of 1-Sperner hypergraphs, a proof that every 1-Sperner hypergraph is both threshold and equilizable, and an efficient algorithm for generating the minimal transversals within this class of hypergraphs. Several applications of 1-Sperner hypergraphs and their structure to graphs will also be discussed, including new characterizations of threshold graphs and new classes of graphs of bounded clique-width.

The talk is based on joint works with Endre Boros and Vladimir Gurvich.
Preprints are available at:
https://arxiv.org/abs/1510.02438
https://arxiv.org/abs/1805.03405

A unique-maximum coloring of a plane graph G is a proper vertex coloring by natural numbers such that each face \alpha of G satisfies the property: the maximal color that appears on \alpha, appears precisely on one vertex of \alpha (or shortly, the maximal color on every face is unique on that face). Fabrici and G\"{o}ring proved that six colors are enough for any plane graph and conjectured that four colors suffice. Thus, this conjecture is a strengthening of the Four Color Theorem. Wendland later decreased the upper bound from six to five.

We first show that the conjecture holds for various subclasses of planar graphs but then we disprove it for planar graphs in general. Thus, the facial unique-maximum chromatic number of the sphere is not four but five. In the second part of the talk, we will consider various new directions and open problems.

(Joint work with Vesna Andova, Bernard Lidick\'y, Borut Lužar, and Kacy Messerschmidt)

The recent notion of quaternionic slice regularity has identified a new class of functions which can play the role of holomorphic (and meromorphic) functions in the quaternionic setting. The talk will present the main basic features of slice regular functions over the quaternions, as well as some of their most curious applications, including those concerning the study of orthogonal complex structures on subsets of the quaternionic space H.

A (1,\le \ell)-identifying code in a digraph D is a dominating subset C of vertices of D such that all distinct subsets of vertices of cardinality at most \ell have distinct closed in-neighbourhoods within C.

In this talk, we give an upper bound on \ell and some sufficient conditions for a digraph of minimum in-degree \delta^-\ge 1 to admit a (1,\le \ell)-identifying code for \ell= \delta^-, \delta^-+1. We give also a new method to obtain an upper bound on \ell for digraphs and graphs using spectral graph theory. As particular cases, we give a characterization of the j-in-regular digraphs admitting a (1,\le \ell)-identifying code for j \in \{1,2\} and \ell\in\{1,2,3\}. We also prove that every k-iterated line digraph of minimum in-degree at least 2 admits a (1,\le \ell)-identifying code with \ell \le 2, and it does not admit a (1,\le \ell)-identifying code for \ell\ge 3. Moreover, we give some bounds of the identifying number of a line digraph, that is, the minimum size of a (1,\le 1)-identifying code.

Nim is an impartial game in which two players take turns choosing a pile and removing a positive tokens from it, with the player making the last move winning. Impartial games are solved by finding which positions are winning and losing, the winning move makes your winning position into a losing position for the opponent. A generalization of winning and losing positions is called the Sprague-Grundy function which partitions positions even further and is needed to know how to play the sum of games. Hypergraph Nim is a new generalization of the game Nim in which instead of a single pile we chose multiple, with our choice of piles denoted by a hypergraph. In this talk we will take a look at the Sprague-Grundy function of Hypergraph Nim.

In earlier work with John Shareshian, we asked whether for every number n, there are primes p and r so that every nontrivial binomial coefficient n choose k is divisible by at least one of the two primes.  The motivation for the question is from group theory: the question is equivalent to that of whether for every n there are primes p,r so that the alternating group A_n is generated by any Sylow subgroups at p and r.  The answer is "yes" up to a set of asymptotic density zero (assuming the Riemann Hypothesis), and we verified a "yes" answer computationally out to 1 billion.

In more recent work, joined by Bob Guralnick, we have verified computationally that a stronger condition holds for all n out to 7 billion.  This computation finishes in a few hours, which is a great improvement over the 2 weeks that our earlier computation out to 1 billion took.

In this talk, I'll overview the interplay between group theory, number theory, and computation allowing this computation.

If we let n(k, d) denote the order of the largest undirected graphs of maximum degree k and diameter d, and let M(k,d) denote the corresponding Moore bound, then n(k,d)\leq M(k,d), for all k\geq 3, d\geq 2. Whilethe inequality has been proved strict for all but very few pairs k and d, the exact relation between the values n(k,d) and M(k,d) is unknown, and the uncertainty of the situation is captured by an open question of Bermond and Bollobas who asked whether it is true that for any positive integer c>0 there exist a pair k and d, such that n(k,d)\leq M(k,d)-c.

In this talk we present a  connection of this question to the value 2\sqrt{k-1}, which is also essential in the definition of the Ramanujan graphs defined as k-regular graphs whose second largest eigenvalue (in modulus) does not exceed 2\sqrt{k-1}. We further reinforce this surprising connection by showing that if the answer to the question of Bermond and Bollobas were negative and there existed a c > 0 such that n(k,d) \geq M(k,d) - c, for all k\geq 3, d\geq 2, then, for any fixed k and all sufficiently large even d's, the largest undirected graphs of degree k and diameter d would have to be Ramanujan graphs. This would imply a positive answer to the open question whether infinitely many non-bipartite k-regular Ramanujan graphs exist for any degree k.

In this talk, we consider secondary construction methods of bent and plateaued functions.

The first part of this talk focuses on plateaued functions, where we analyse the concept of its dual. In contrary to bent functions, for which the dual is well established, the dual of a plateaued functions never received enough attention. Using suitable ordering(s) in combination with signs of non-zero entries of the Walsh spectra of a plateaued function, we show that new characterization of plateaued functions can be derived. In addition, these results will lead to completely new approach (so-called Spectral method) for construction of cryptographically significant Boolean functions. 

The second part of the talk focuses on secondary constructions of bent and plateaued functions. As we noticed that almost all secondary constructions deduced in the last four decades can be generalized using the composition of one Boolean (usually plateaued) and one vectorial function, we show how one can generalize almost all known secondary construction methods of bent and plateaued functions, by applying the concept of the dual developed for plateaued functions. The so-called “composite representation” of Boolean functions gives a better understanding of the existing secondary constructions and it also allows us to provide a general construction framework of these objects.

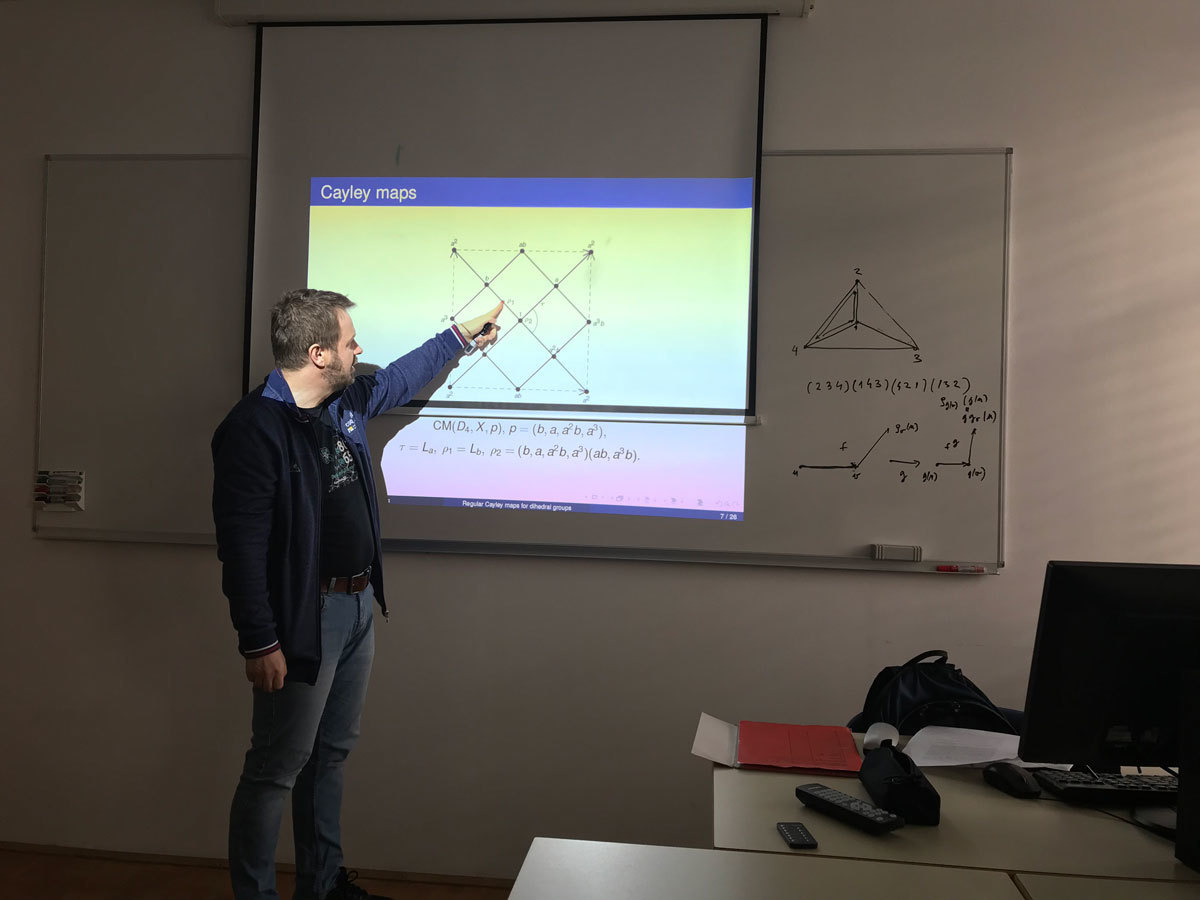
A combinatorial map is a pair M=(X,r), where X is a finite simple connected graph and r is a permutation of its arcs (directed edges) such that the orbit of the arc (u,v) under r is the set of arcs emanating from u. Aut(M) consists of the automorphisms of X for which the induced permutations on the arcs commute with r. The order |Aut(M)| is less than equal to 2|E(G)|, and when equality holds M is called regular. M is a Cayley map for a finite group G if X=Cay(G,S), and r is defined by (h,g) -> (h,p(h^{-1}g)), where h^{-1} \in S and p is a fixed cyclic permutation of S.  Regular Cayley maps for cyclic groups were classified by Conder and Tucker (Trans. Amer. Math. Soc., 2014). In this talk, I will show the classification of regular Cayley maps for dihedral groups.

The talk provides a brief introduction to routing games and related game theory concepts. We will discuss different variants and simple examples.

In the second part of the talk, we will look at a dynamic routing game with a special forwarding policy in which a player's priority depends on the previous edge of the chosen path. We present properties and efficiency of equilibria and we specify an algorithm for their calculation. Finally, we give some additional results and open problems.

We briefly present the theory of slice-regular functions of one quaternionic variable and compare this regularity properties with Fueter regular functions (the regularity used physics).

We give a possible extension for shears and overshears in the case of two non-commutative (quaternionic) variables in relation with the associated vector fields and flows. We present a possible definition of volume preserving automorphisms, even though there is no quaternionic volume form on \mathbb{H}^2.

Using this, we determine a class of quaternionic automorphisms for which  the Andersen-Lempert theory applies. Finally, we exhibit an example of a quaternionic  automorphism, which is not in the closure of the set of finite compositions of volume preserving quaternionic shears, though its restriction to complex subspace is in the closure of the set of finite compositions of volume preserving complex shears.

Majorana theory was introduced by A. A. Ivanov as an axiomatic framework in which to study objects related to the Monster group and its 196884 dimensional representation, the Griess algebra. The objects at the centre of the theory are known as Majorana algebras and can be studied either in their own right or as Majorana representations of certain groups. I will give a brief introduction to the theory before presenting the methods and results of my recent work developing an algorithm to construct the Majorana representations of a given group. 

This work is based on a paper by Á. Seress and is joint with M. Pfeiffer.

The concept of k-regular maps was introduced into topology by Karol Borsuk in 1950'. Long before it was investigeted in interpolation and approximation theory by (among others) Chebyshev and Kolmogorov, and had distinctly applied mathematics flavor.

A continuous map f: X\to V, from a topological space to a vector space is k-regular of for any k distinct points in X their images are linearly independent.

Example: 
If f:X\to V is an embedding, then the map F: X\to R\oplus V, defned by F(x)=(1,f(x))
is 2-regular.

In analogy to theory of embeddings, one of central problems in the study of k-regular maps is (given k, X)  to construct a k-regular map of X into space V of minimal possible dimension. Unlike for embeddings, this is interesting already for X=R^d I will discuss  lower bounds (obstructions) to the existence to the existence of k-regular maps (this involves some algebraic topology of configuration spaces, following work of many people, most recent being Blagojevic, Cohen, Lueck and Ziegler) and upper bounds (constructions) (this involves some algebraic geometry of secant varieties and  Hilbert schemes, following the work of Buczynski, Januszkiewicz, Jelisiejew and Michalek).

In 2017 we have been hearing a lot about blockchain, in 2018 a bit less. But what is a blockchain, really? How is it connected to Bitcoin? Why is there the "crypto" in "cryptocurrencies"? And should we, as mathematicians, be even interested in it? We will be talking about these and similar questions during the seminar. We will briefly look at what kind of mathematics a usual blockchain is based on, how it started, and in what ways today's world is trying to use it.

In this talk we present an algorithm for computing the Wiener index of a tree from the distance matrix of its leaves, known also as the terminal matrix of a tree. The algorithm performs better than the linear time algorithm for trees that have a large number of vertices of valence 2.