Raziskovalni matematični seminar - Arhiv

The research field of Inverse Problems has witnessed a tremendous growth in recent years, due to its ability to capture and tackle complex problems occuring in real-world applications. However, numerous inverse problems are ill-posed.

Depending on the nature of the problem, various approaches can be considered for stable approximation of the solution. This talk discusses variational and iterative regularization approaches, with emphasis on reconstructing nonnegative solutions when nonnegative data are available.

For positive integers n \ge 2k, the Kneser graph KG(n, k) has as vertices the k-subsets of [n] = {1,...,n} and two vertices are connected by an edge if they have empty intersection. In particular, for s \ge 2, the s-stable Kneser graph is the subgraph of KG(n, k) induced by the k-subsets S of [n] such that the circular distance between any two elements in S is at least s. For this graph class there are several open problems, among them the hom-idempotence and finding its chromatic number. Some papers solve these problems in particular instances, but the general case remains open. In this talk we show some conjectures and advances on them.

SLIDES from the talk are here.

In 1955 Gerhard Ringel introduced the notion of Hamilton Surface Decomposition. 30 years later he wrote two more papers with Nora Hartsfield and Brad Jackson on the same topic. Approximately at the same time I wrote a manuscript together with Brian Alspach. Our result generalizes a lot Ringel’s original result. About 30 years we were polishing the paper, even with help of Alen Orbanić. The purpose of this talk is to test whether the paper is ready to be published.

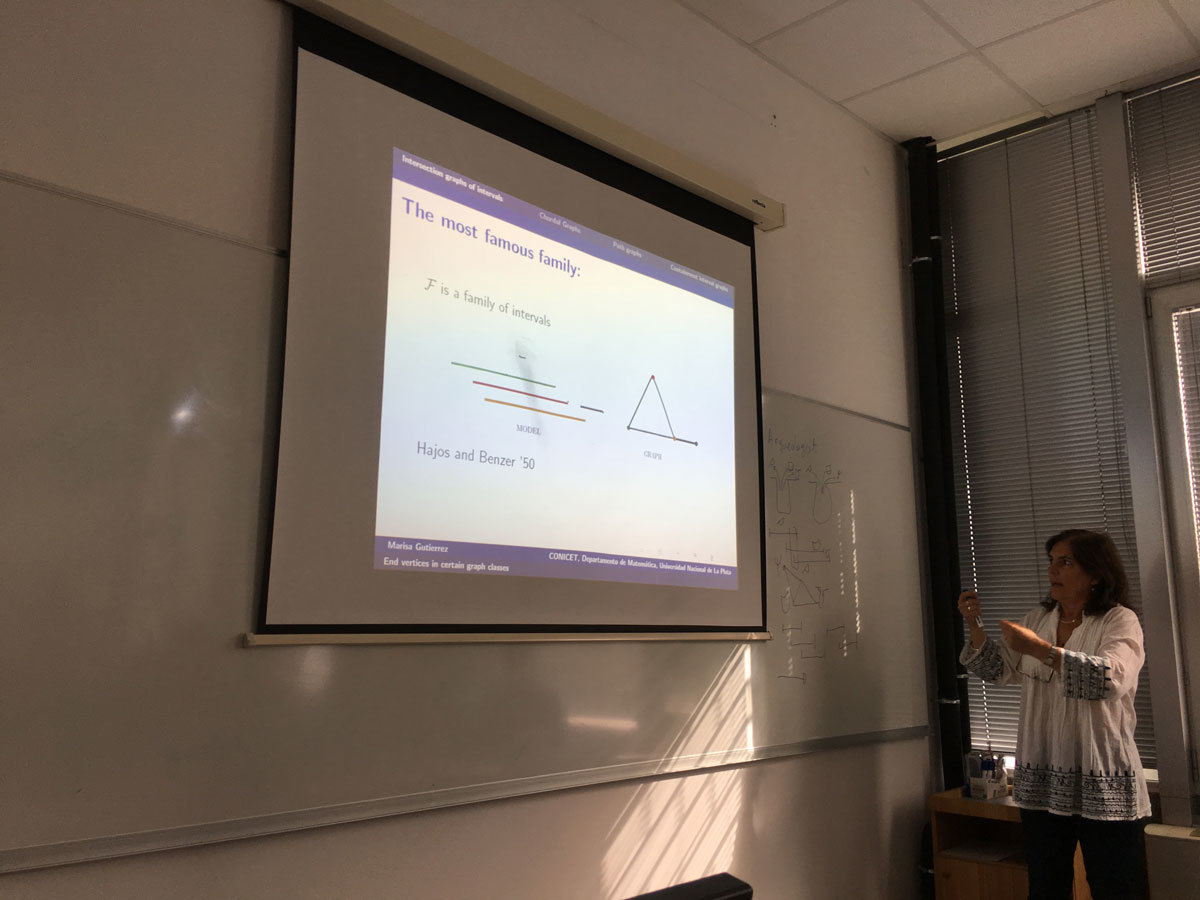
Given a finite family of non empty sets F =(A_i)_{i\in I} it is possible define two graphs associated with the family: the intersection graph of F with set of vertices I and such that two vertices i, j are adjacent if and only if A_i∩A_j \ne \emptyset; and the containment graph of F in which I is also the vertex set but two vertices i, j are adjacent if and only if A_i ⊂ Aj or Aj ⊂ Ai. In both cases F is a model of G.

Different classes of graphs can be defined by considering special classes of sets. For example interval graphs are the intersection graphs of intervals of the real line. The path graphs are the intersection graphs of paths in a tree. These graphs have aroused great attention because storing and accessing the structured information of a graph can be made more efficiently if this is the graph of Intersection of families with good properties [2]. On the other hand, the CI graphs that are the containment graphs of intervals of the real line are studied.

In any case it is natural ask which are the vertices of the graph that can be end vertices in the model? An end vertex v of an interval graph is one such that there is a model of the graph such that Av is more to the left in the model. Gimbel [1] totally characterizes these vertices given forbidden vertices in a family of graphs.

In this work we give these kind of characterizations for leaves vertices in the path graphs [3] and end vertices in containment graphs [4].

Bibliography:
[1] J. Gimbel, End vertices in interval graphs, Discrete Applied Mathematics 21 (1988) 257-259.
[2] J.Spinrad, Efficient Graph Representations, American Mathematical Society (2003) USA.
[3] M. Gutierrez and S. Tondato, End simplicial vertices in path graphs. Discussions Mathematicae Graph Theory. In press (2016).
[4] L. Alcon, N. Gudino and M. Gutierrez, End vertices in containment interval graphs. In process.