Raziskovalni matematični seminar - Arhiv

A Hadamard matrix of order m is a (m \times m) matrix H=( h_{i,j}), h_{i,j} \in \{ -1,1 \}, satisfying HH^T=H^TH=mI_m, where I_m is an (m \times m) identity matrix. A Hadamard matrix is called regular if the row and column sums are constant. It is conjectured that a regular Hadamard matrix of order 4k^2 exists for every positive integer k. We will give some method of constructing regular Hadamard matrices and related self-orthogonal codes.

The Moore bound M(k,g) is a lower bound on the order of k-regular graphs of girth g (denoted (k,g)-graphs). The excess e of a (k,g)-graph of order n is the difference n-M(k,g). We consider the existence of (k,g)-bipartite graphs of excess 4 by studying spectral properties of their adjacency matrices.

For a given graph G and for the integers i with 0\leq i\leq diam(G), the i-distance matrix A_i of G is an n\times n matrix such that the entry in position (u,v) is 1 if the distance between the vertices u and v is i, and zero otherwise.

We prove that the (k,g)-bipartite graphs of excess 4 satisfy the equation kJ=(A+kI)(H_{d-1}(A)+E), where A=A_{1} denotes the adjacency matrix of the graph in question, J the n \times n all-ones matrix, E=A_{d+1} the adjacency matrix of a union of vertex-disjoint cycles, and H_{d-1}(x) is the Dickson polynomial of the second kind with parameter k-1 and degree d-1. We observe that the eigenvalues other than \pm k of these graphs are roots of the polynomials H_{d-1}(x)+\lambda, where \lambda is an eigenvalue of E.

Based on the irreducibility of $H_{d-1}(x)\pm2$, we give necessary conditions for the existence of these graphs. If E is the adjacency matrix of a cycle of order n, we call the corresponding graphs {graphs with cyclic excess; if E is the adjacency matrix of a disjoint union of two cycles, we call the corresponding graphs graphs with bicyclic excess. We prove the non-existence of (k,g)-graphs with cyclic excess 4 if k\geq 6 and k \equiv 1 \pmod 3, g=8, 12, 16 or k \equiv 2  \pmod 3, g=8; and the non-existence of (k,g)-graphs with bicyclic excess 4 if k\geq 7 is an odd number and g=2d such that d\geq 4 is even.

Let G be a graph with a proper vertex colouring. Let a and b be two of the colours. Then a connected component of the subgraph induced by those vertices coloured either a or b is known as a Kempe chain. Another proper colouring of G can be obtained by swapping the colours on the vertices of a Kempe chain. This colouring is said to have been obtained by a Kempe change. Two colourings of G are Kempe equivalent if one can be obtained from the other by a sequence of Kempe changes.

Kempe chains were introduced by Alfred Kempe in an attempt to prove the Four Colour Theorem. Though this attempt failed, the method of Kempe chains was used in the proof of the Five Colour Theorem and elsewhere.

We address a 2007 conjecture of Bojan Mohar that asserts that, for k at least 3, all k-colourings of a k-regular graph that is not complete are Kempe equivalent. We show that the conjecture holds with one exception, the triangular prism.

This is joint work with Marthe Bonamy, Nicolas Bousquet, Carl Feghali and Daniel Paulusma.​

The Colouring problem is that of deciding, given a graph G and an integer k, whether G admits a (proper) k-colouring. For all graphs H up to five vertices, we classify the computational complexity of Colouring for (diamond,H)-free graphs. Our proof is based on combining known results together with proving that the clique-width is bounded for (diamond,P_1+2P_2)-free graphs. Our technique for handling this case is to reduce the graph under consideration to a k-partite graph that has a very specific decomposition. As a by-product of this general technique we are also able to prove boundedness of clique-width for four other classes of (H1,H2)-free graphs. As such, our work also continues a systematic study into the (un)boundedness of clique-width of (H_1,H_2)-free graphs.

Joint work with Konrad Dabrowski and François Dross.

The aim of this talk is to analyze poor performance of Slovenia at the ERC grant calls. In particular, we will present five major errors in the scientific policy in Mathematics in Slovenia over a span of several decades. We will also point out some other reasons for underperformance of Slovenia and other EU13 countries.

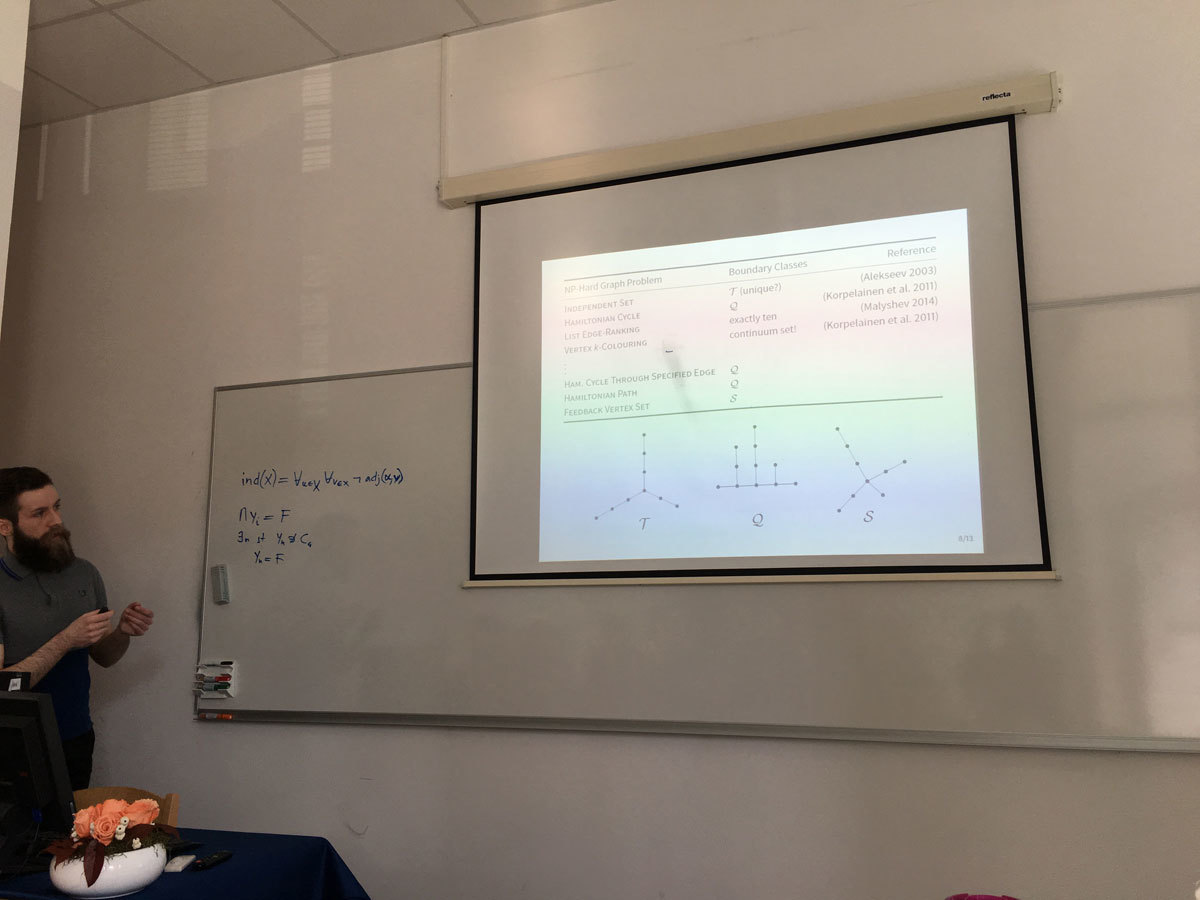
Many NP-hard graph problems remain NP-hard even for restricted classes of graphs, while they become polynomial-time solvable when further restrictions are applied. It is therefore natural to ask when a certain "hard" graph problem becomes "easy": Is there any "boundary" separating "easy" and "hard" instances? Alekseev considered this question in the case the instances are hereditary classes of graphs.

Given a graph problem Pi, a hereditary class of graphs X is Pi-hard if Pi is NP-hard for X, and Pi-easy if Pi is solvable in polynomial time for graphs in X. He introduced the notion of Pi-boundary class, playing the role of the "boundary" separating Pi-hard and Pi-easy instances, and showed that a finitely defined (hereditary) class is Pi-hard if and only if it contains a Pi-boundary class. Moreover, he determined a boundary class for Independent Set, the first result in the systematic study of boundary classes for NP-hard graph problems. 

In the talk, I will review some known results and present new boundary classes for some problems involving non-local properties, like Hamiltonian Path and Feedback Vertex Set.