Raziskovalni matematični seminar - Arhiv

The family of generalized Petersen graphs G(n,k), introduced by Coxeter et al. [Coxeter, H. et al. (1950), ‘Self-dual configurations and regular graphs’, Bull. Amer. Math.Soc 56, 413--455.] and named by Mark Watkins (1969), is a family of cubic graphs formed by connecting the vertices of a regular polygon to the corresponding vertices of a star polygon. The Kronecker cover KC(G) of a simple undirected graph G is a special type of bipartite covering graph of G, isomorphic to the direct (tensor) product of G and K2. We characterize all the members of generalized Petersen graphs that are Kronecker covers, and describe the structure of their respective quotients. We observe that some of such quotients are again generalized Petersen graphs, and describe all such pairs.

The Weiss Conjecture has stimulated much study of symmetric graphs, especially concerning the order of vertex-stabilisers. The conjecture roughly asserts that in a locally-primitive symmetric graph, the vertex-stabiliser is not too large compared to the valency. The conjecture implies that “local properties” have a global impact, since this also bounds the order of the automorphism group. Further refinements to this conjecture were suggested, first by Praeger who asked if local quasiprimitivity might be sufficient, and then by Potocnik-Spiga-Verret who found semiprimitive groups are the key. This latter class of permutation groups has not been well studied, and indeed only recently - 2008 - appeared in the literature. In seeking to understand the validity of these conjectures, I have been motivated to study semiprimitive groups in a more general context, and try to make our understanding of this class of groups equal to that of the well studied class of primitive groups. In this talk I’ll mention some progress towards that, and highlight the impact the results have already had on the aforementioned conjectures.

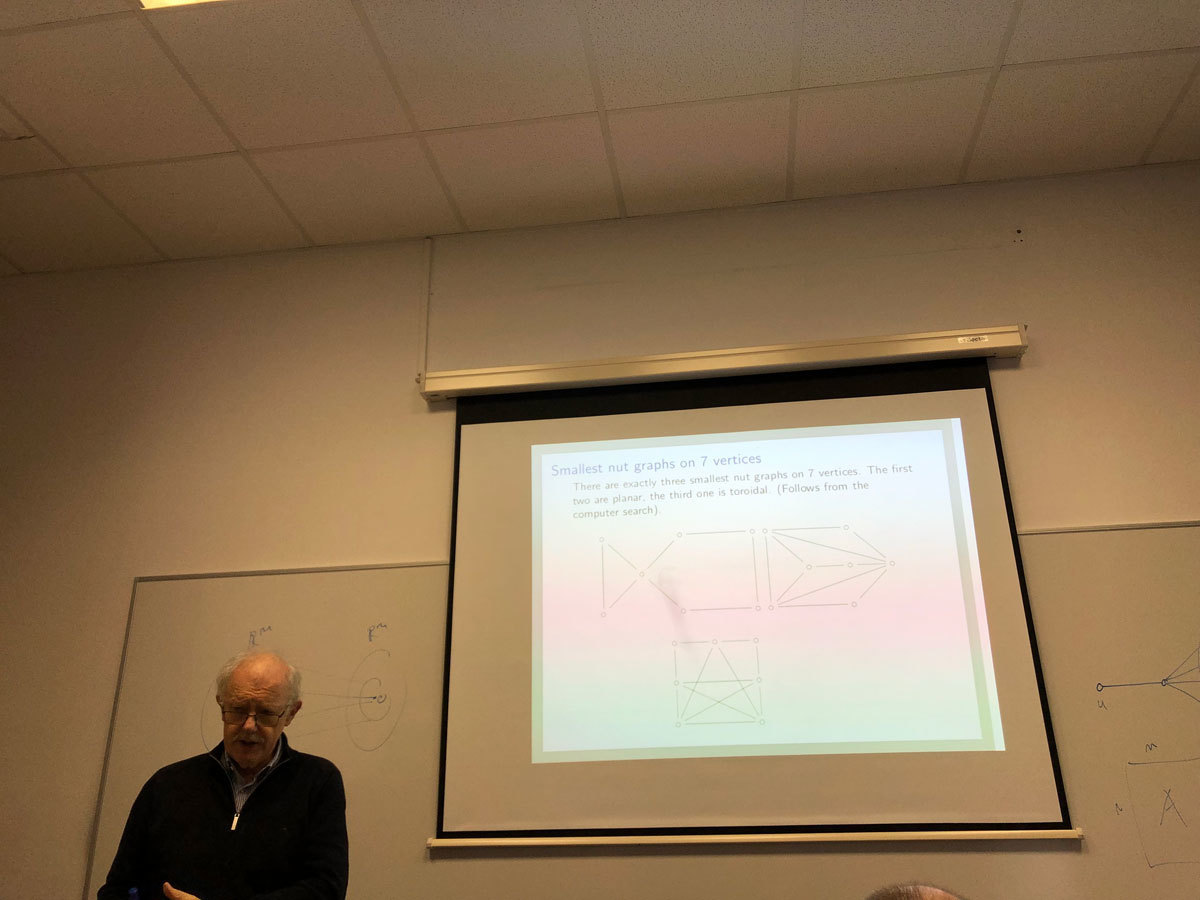
A nut graph is a singular graph of nullity one with a kernel eigenvector having no component equal to 0. We attack the following problem. For each valence d, determine all values of n such that a regular, d-valent nut graph of order n exists. We solve this problem completely for d \leq 4. The main tool in our approach is the Fowler extension of a graph. If time permits we will also give a demonstration of a short sagemath program that tests whether a given graph is a nut graph. This talk is based on the work in progress with John Baptist Gauci and Irene Sciriha. In the proof of case d=4 the help of Patrick Fowler and Nino Bašić is acknowledged.