Raziskovalni matematični seminar - Arhiv

For a given graph search algorithm and a graph G, a vertex v is said to be an end-vertex if there exists a corresponding search ordering of the vertices such that v is the last vertex in this ordering. It is known that the complexity of recognizing the end-vertices in general graphs is NP-hard for several search algorithms, such as Breadth First Search, Depth First Search, and their lexicographic variants. This motivated the study of end-vertices with respect to some other search algorithms. In this work we consider Maximum Cardinality Search (MCS) and Maximum Neighborhood Search (MNS) and present results concerning the complexity of the end-vertex problem with respect to these search methods. We give some proofs of NP-completeness of this problem in general graphs, as well as polynomial-time algorithms, when a graph is restricted to belong to certain graph classes. Joint work with J. Beisegel, C. Denkert, E. Köhler, M. Krnc, R. Scheffler, and M. Strehler.

We consider a bi-level knapsack problem, where two players, the leader and the follower, are each associated with a subset of the items. The leader may offer profits for its items to the follower, before the follower selects a subset of all items in order to utilize a bounded resource in the best possible way, i.e. trying to maximize the overall profit.

The leader receives as pay-off only the profits from those items of its associated subset that were included in the overall solution chosen by the follower. This pay-off is then reduced by the profits offered to the follower. The resulting setting is a Stackelberg strategic game. The leader has to resolve the trade-off between offering high profits as incentives to the follower and offering low profits to gain high pay-offs.

We analyse the problem for the case where the follower solves the resulting knapsack problem to optimality, and obtain a number of strong complexity results. Then we invoke a typical assumption of the literature that the follower's computation power is bounded. Under this condition, we study three natural Greedy-type heuristics applied by the follower. The solution structures and complexities of the resulting problems are investigated and solution strategies are derived, in particular an ILP model, but also (pseudo)polynomial algorithms, when possible.

Joint work with Gaia Nicosia, Andrea Pacifici and Joachim Schauer

Matrices whose commutant is either maximal or minimal with respect to set-inclusion were classified in 2005 by Dolinar and Šemrl in their pursuit towards classification of bijections which preserve zeros of Lie product. The classification which they obtained  is valid only for complex matrices. Recently, we extended their classification in several directions:
(a) For matrices over an arbitrary field. Besides the  classes that were obtained in the complex case some new possibilities are possible here.
(b) We also investigated problems of these kinds within certain subclasses of (complex) matrices, in particular within doubly stochastic matrices.
(c) Instead of commutativity one may further consider the commutativity up to a factor \xi, defined by AB = \xi BA and classify matrices which are extremal with respect to this relation.

The aim of the talk is to present the obtained results. This is joint work with many collaborators.

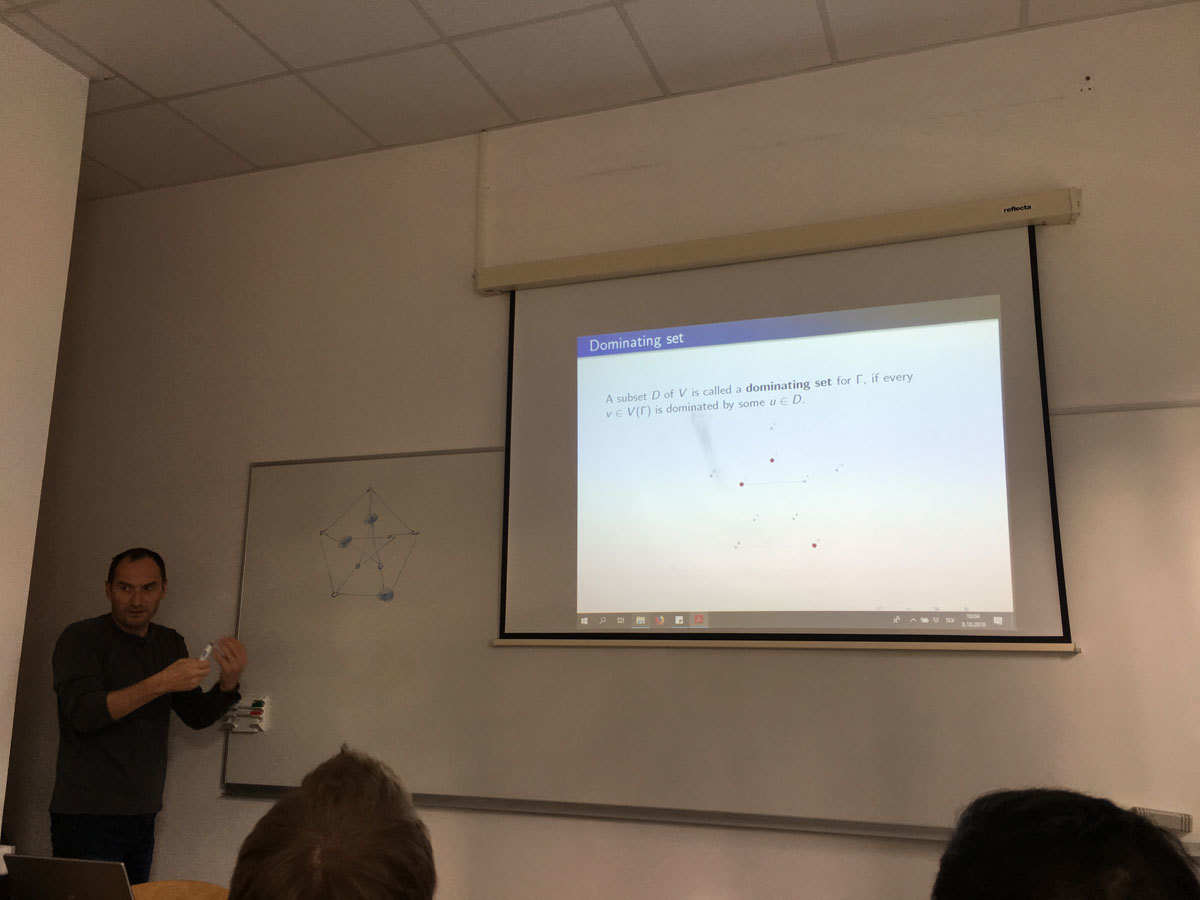
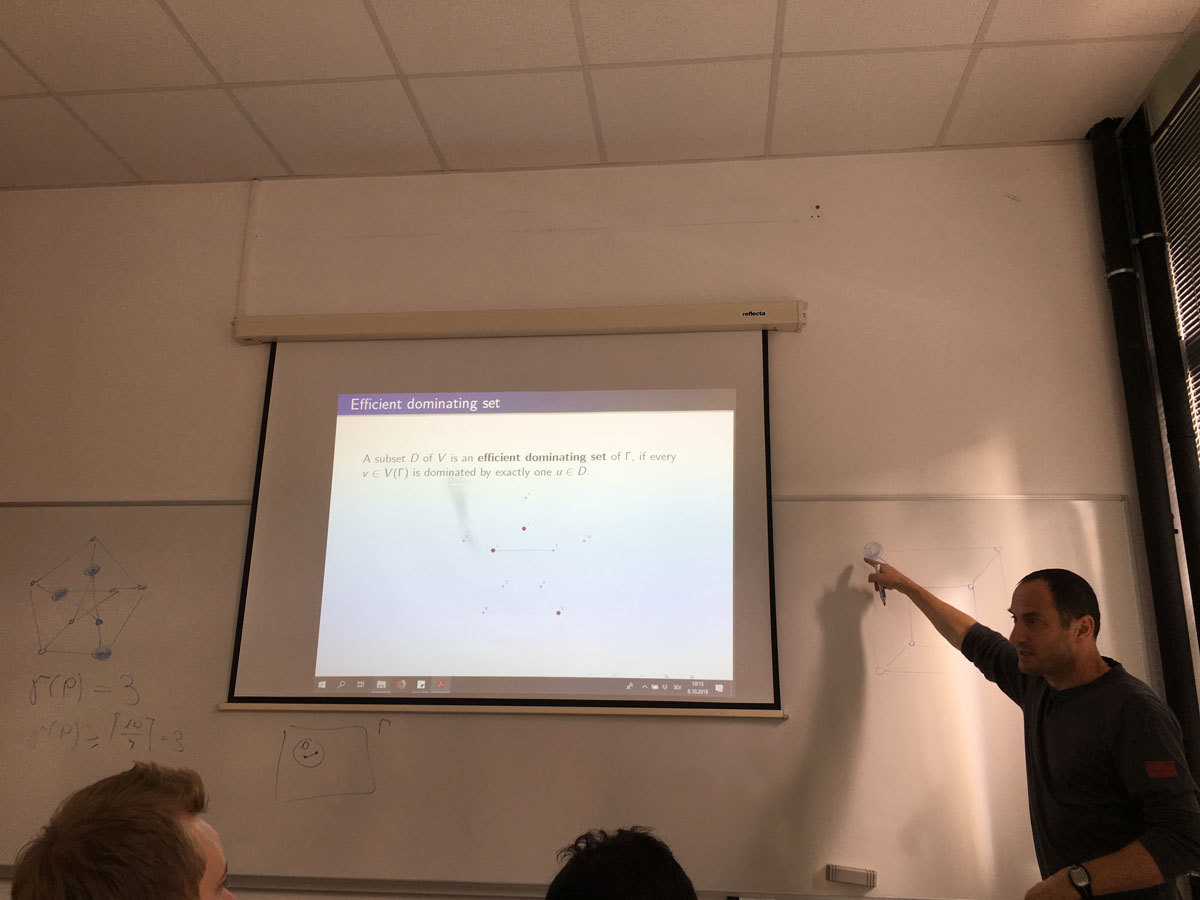
An independent set D of vertices in a graph is an efficient dominating set when each vertex not in D is adjacent to exactly one vertex in D. In this talk we give a classification of cubic and quartic Cayley graphs on abelian groups, which admit efficient dominating set.

Joint work with Sibel Ozkan and Cafer Celiskan.

Determining the genus of graphs is one of the fundamental NP-complete problems. Thus it makes sense to ask whether the genus can be efficiently approximated. By using the Szemeredi Regularity Lemma, and by analysing the genus of random and quasirandom graphs, we are able to find a PTAS (polynomial-time approximation scheme) to approximate the genus of dense graphs within arbitrarily small error.

This is joint work with Yifan Jing.