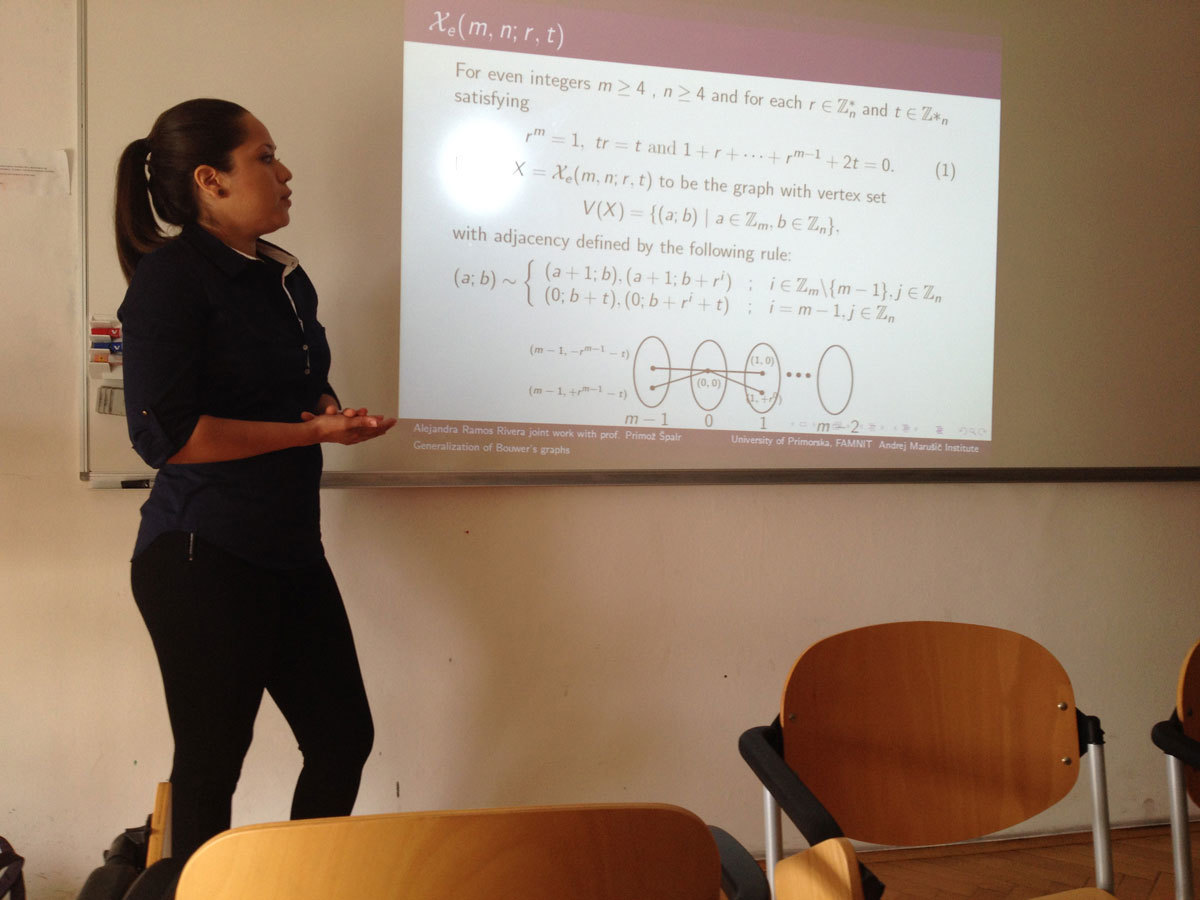Raziskovalni matematični seminar - Arhiv

The domination game is played on a graph $G$ by two players, Dominator and Staller. They are alternating turns in choosing vertices, one at a time, so that each chosen vertex enlarges the set of vertices of $G$ dominated to that point in the game. The game ends when all vertices of $G$ are dominated. The aim of Dominator is that the game ends in as few moves as possible, while Staller's goal is to maximize the number of moves. Assuming that both players play optimally, and that Dominator starts the game, the number of vertices chosen in the game is called the game domination number, $gamma_g(G)$; if Staller starts the game, we denote the resulting number of moves by $gamma_g'(G)$.

The domination game was introduced in 2010, and received a considerable attention by several authors. In this talk, I intend to give a brief overview of the results and methods related to the domination game. In particular, $3/5$-conjectures, relations between both versions of the game, and complexity issues will be presented.

In the attempt of solving the isoperimetric problem in 1838 Steiner missed the important point of the existence of the solution. Various authors found alternative proofs or filled the gap. W. Gross belongs to the second group (1917). He constructed, given a convex body K, a sequence of directions {u_n} such that iterated Steiner symmetrals taken in that directions minimize the perimeter and converge, in the Hausdorff distance, to the ball K^* centered at the origin and having the same volume as K.

Peter Mani (1986) was the first to understand that the convergence of iterated Steiner symmetrizations of a convex body K to K^* holds almost surely and conjectured that this happens also if we consider successive Steiner symmetrizations of a compact set. The conjecture was confirmed in 2006 by van Schaftingen. I provided in 2013 a different proof.

I conjectured in 2009 that density alone of the sequence {u_n} is sufficient for the convergence of the iterated Steiner symmetrization. P. Gronchi disproved the conjecture in 2010.

Bianchi, Klain, Lutwak, Yang and Zhang (2011) proved however the following result:

Theorem. If K is a convex body and U is a countable and dense set of directions, then it can be ordered in a sequence {u_n} such that the successive Steiner iterations of K in that directions converge in the Hausdorff metric to the ball K^*.

I improved recently this result in two directions (2015, visible on line). On one hand the seed K of the iteration is allowed to be compact rather than just convex, and moreover there exists a universal ordering of U which works for every seed.

In the talk we will describe the recent result of the speaker how to construct a holomorphic function on the open unit ball B_N of C^N, N>1, whose real part is unbounded on every path in B_N of finite length that ends on bB_N. Level sets of such functions are examples of complete complex hypersurfaces in the ball and give a complete answer to a question of P. Yang from 1977 about the existence of bounded complete complex manifods. We will also present a generalization of this result to pseudoconvex domains in C^N and a related result obtained jointly with A. Alarcon and F. J. Lopez about a construction of a complete proper holomorphic embedding from the open unit disc in C to B_2.

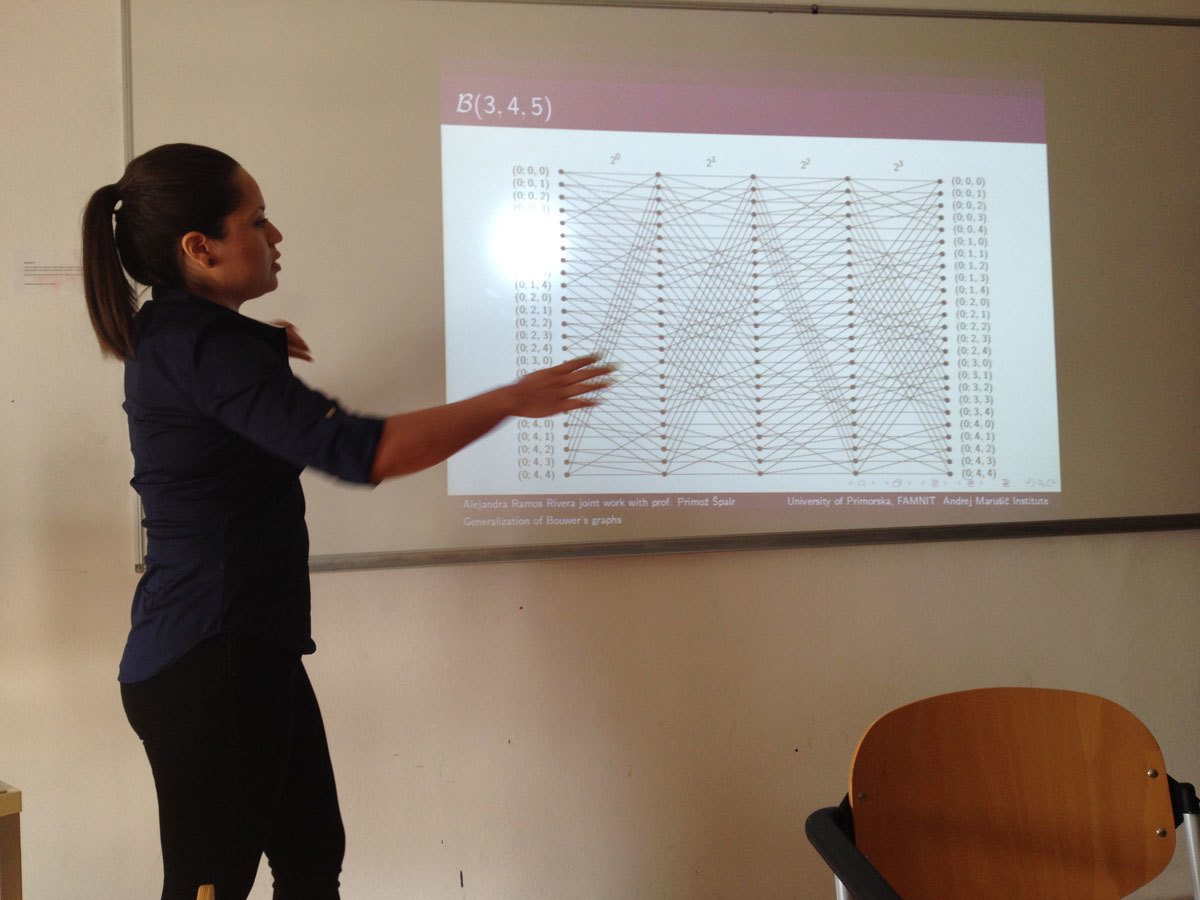
Bouwer proved that there exists a half-transitive graph of every even valency greater that 2, by giving a contruction for a family of graphs now known as B(k,m,n). Recently, it was proved by M. Conder and A. Žitnik which of Bower’s graphs are half-arc-transitive.

Let D_G(X) be one of the two opposedly oriented digraphs associated with a half-transitive graph X with respect to the action of Aut(X). Two arcs are related if they have the same initial vertex (tail), or the same terminal vertex (head). The subgraphs consisting of equivalence classes of directed edges of this relation are called alternets.

Let {\cal A} = {A_i | i\in {1, 2, ... ,m}} be the set of alternets in X and for each i\in {1, 2, . . . ,m} define H_i to be the set of all vertices at the heads of arcs in A_i\in{\cal A}, and T_i be the set of all vertices at the tail of arcs in A_i. If H_i = T_j for some i, j\in {1, 2, ... ,m}, then X is said to be tightly attached. Tightly attached graphs with valency 4 were classified by P. Šparl and D. Marušič.

In this talk a family of tightly attached half-transitive graphs with valency 2k is introduced as a generalization of the Bouwer’s graphs. 

Based on joint work with Primož Šparl.