Raziskovalni matematični seminar - Arhiv

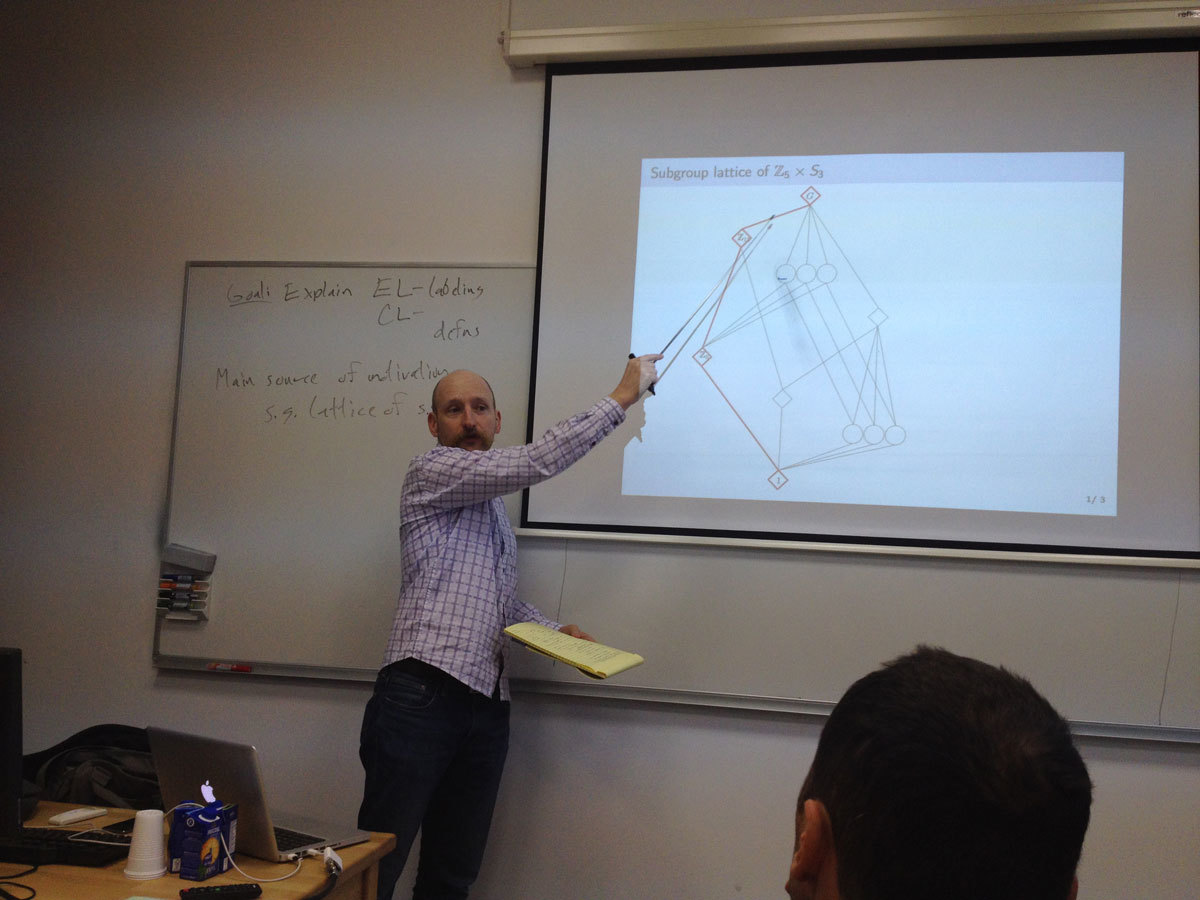
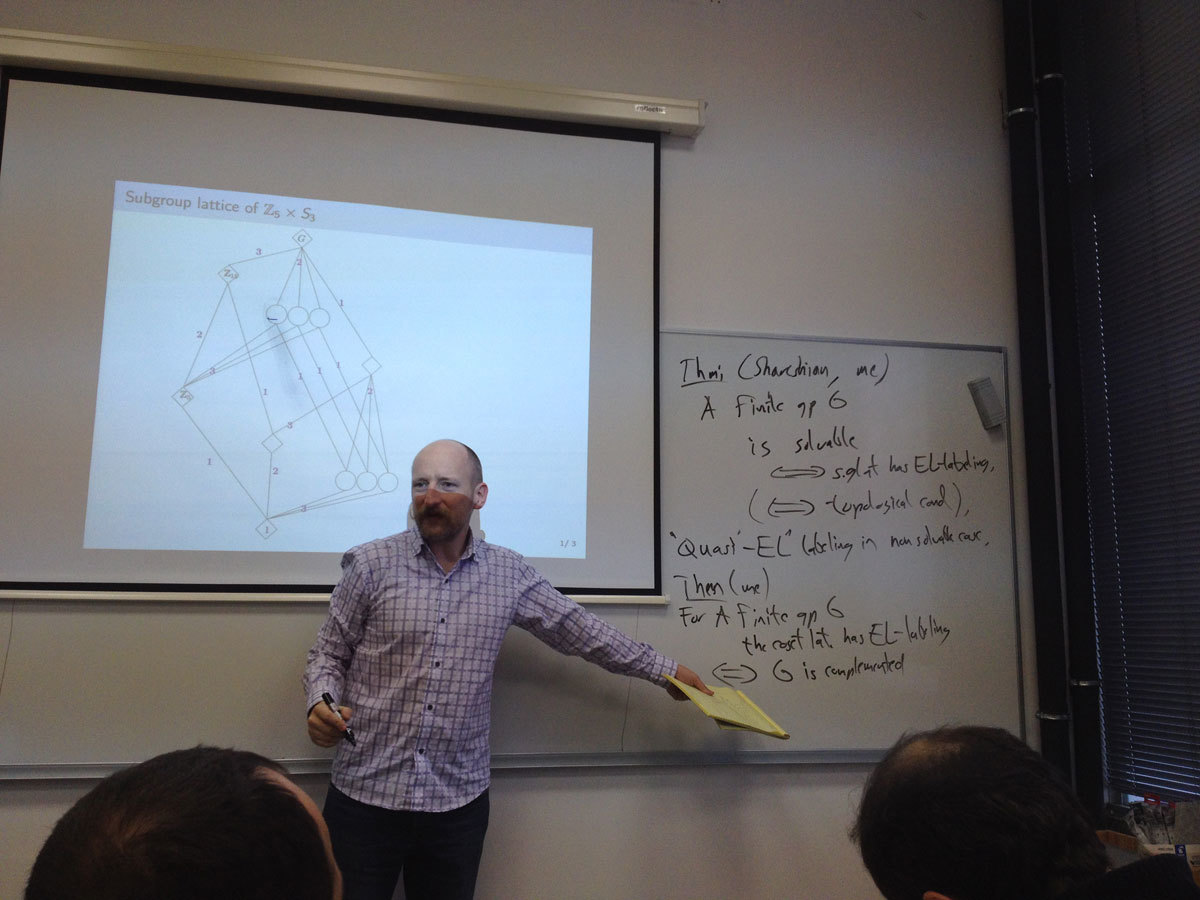
This talk will be about finite lattices and posets.  I'll tell you what an EL-labeling is, explain how the subgroup lattice of a supersolvable group motivates its definition, and give related results on lattices defined from groups. Unfortunately, EL-labelings can be difficult to construct, and there are several lattices for which it is not known whether an EL-labeling exists.  I'll show how this leads to the idea of a CL-labeling.

My goal, if time allows, is to give a clear idea of recent work of myself and Jay Schweig, in which we show that a certain wide class of lattices has a CL-labeling.

A clique in a graph is said to be strong if it intersects every maximal stable set. A graph is called localizable if it admits a partition of its vertex set into strong cliques. In this talk I will present some results regarding the complexity of recognizing localizable graphs. We will discuss when is the product (lexicographic or Cartesian) of two graphs localizable.

We will also discuss what does it mean for a vertex-transitive graph to have a strong clique.

This is a joint work with Martin Milanič and Bernard Ries.

A Cayley map M=CM(G,X,P) is an embedding of a Cayley graph C(G,X) in an orientable surface with the property that each left multiplication by an element of G becomes a map automorphism of M: G < Aut(M). A  Cayley map CM(G,X,P) is regular (i.e., its orientation preserving automorphisms act regularly on darts) if and only if a skew-morphism exists that has an orbit X on which it is equal to P. 

With Roman Nedela we asked the question whether the skew-morphisms which do not have this property are good for anything, and arrived at the concept of a half-regular Cayley map.