Raziskovalni matematični seminar - Arhiv

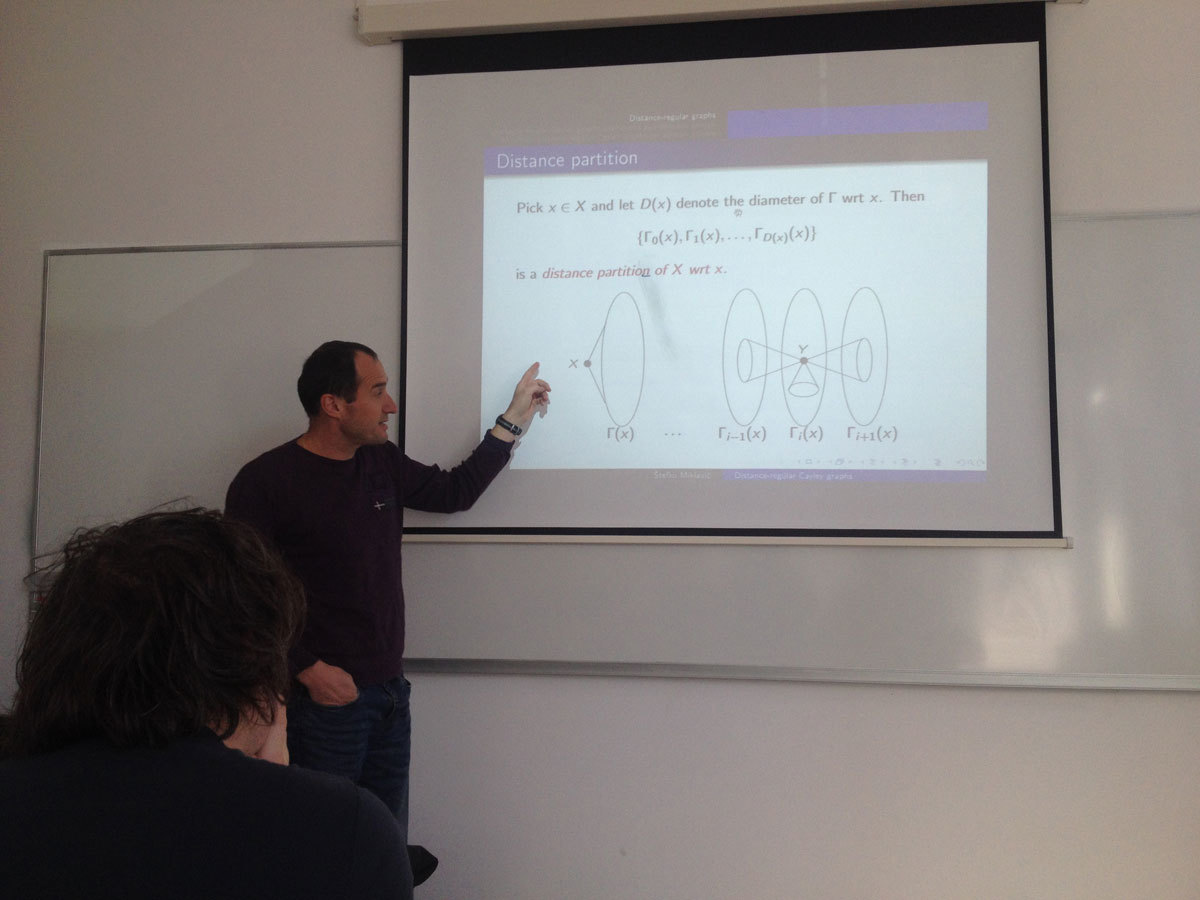
In this talk we consider the following problem: for a given class of groups ${\cal G}$, classify distance-regular Cayley graphs $Cay(G;S)$, where $G \in {\cal G}$.

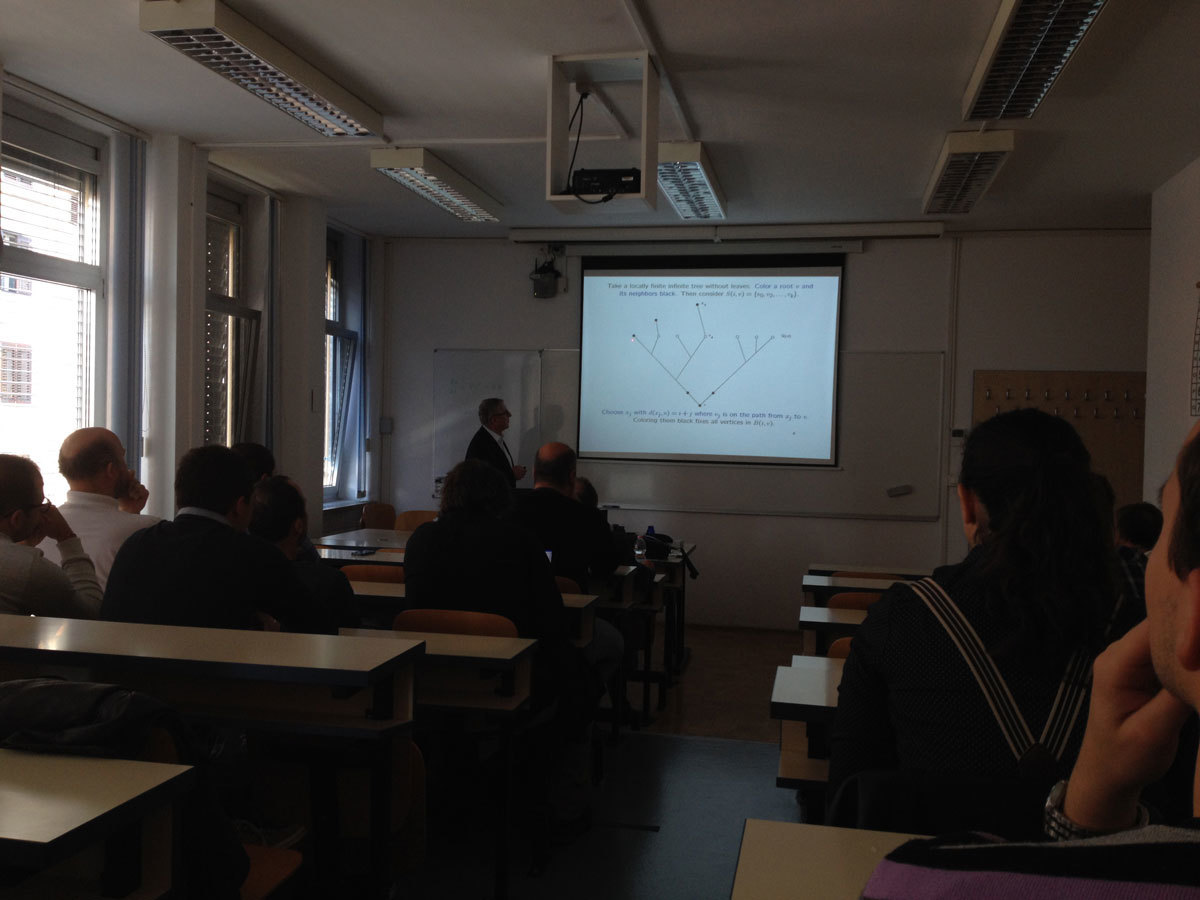
In a graph, a set of vertices that is stabilized setwise by only the trivial automorphism is called a distinguishing set. Tom Tucker conjectured that every connected, infinite locally finite graph G has such a set if each nontrivial automorphism of G moves infinitely many vertices. The conjecture is know as the Infinite Motion Conjecture, which is still open despite the fact that numerous large classes of graphs have been shown to satisfy it. 

In finite graphs distinguishing sets, if they exist, can be very small in comparison to the size of the graph, and in infinite graphs such sets can be finite. If they are not finite, their density can be zero. 

This talk introduces to  the subject and presents new results about the density of distinguishing sets and the  Infinite Motion Conjecture.

In this talk I give necessary and sufficient conditions for when a system of nonlinear delay equations can be reduced to a system of ordinary differential equations. The class of systems considered contains nonlinear models of physiologically structured populations.

 My talk is based on joint work (in progress) with Odo Diekmann and Hans Metz.

An automorphism (or symmetry) of a combinatorial graph may be called even or odd according to whether it acts as an even or odd permutation on the vertices of the graph. In this talk, I will present a partial result about the following question: When does the existence of even automorphisms of a graph force existence of odd automorphisms? In particular, I will present complete information the on existence of odd automorphisms for cubic symmetric graphs.

'Maniplex' is a generalization of 'polytope' and is at the same time a generalization of 'map'.  We are interested in those which have large symmetry groups, and these come in two kinds, 'rotary' and 'reflexible', both called 'regular' by some faction of the community.  In this talk, we will introduce manilexes, talk about the motivations for the definition, give some basic examples of several dimensions, and discuss the distinction between maniplexes and polytopes.  Our main goal is to understand a handful of operators (Dual, Petrie, Bubble, Twist) which transform one regular maniplex into another.

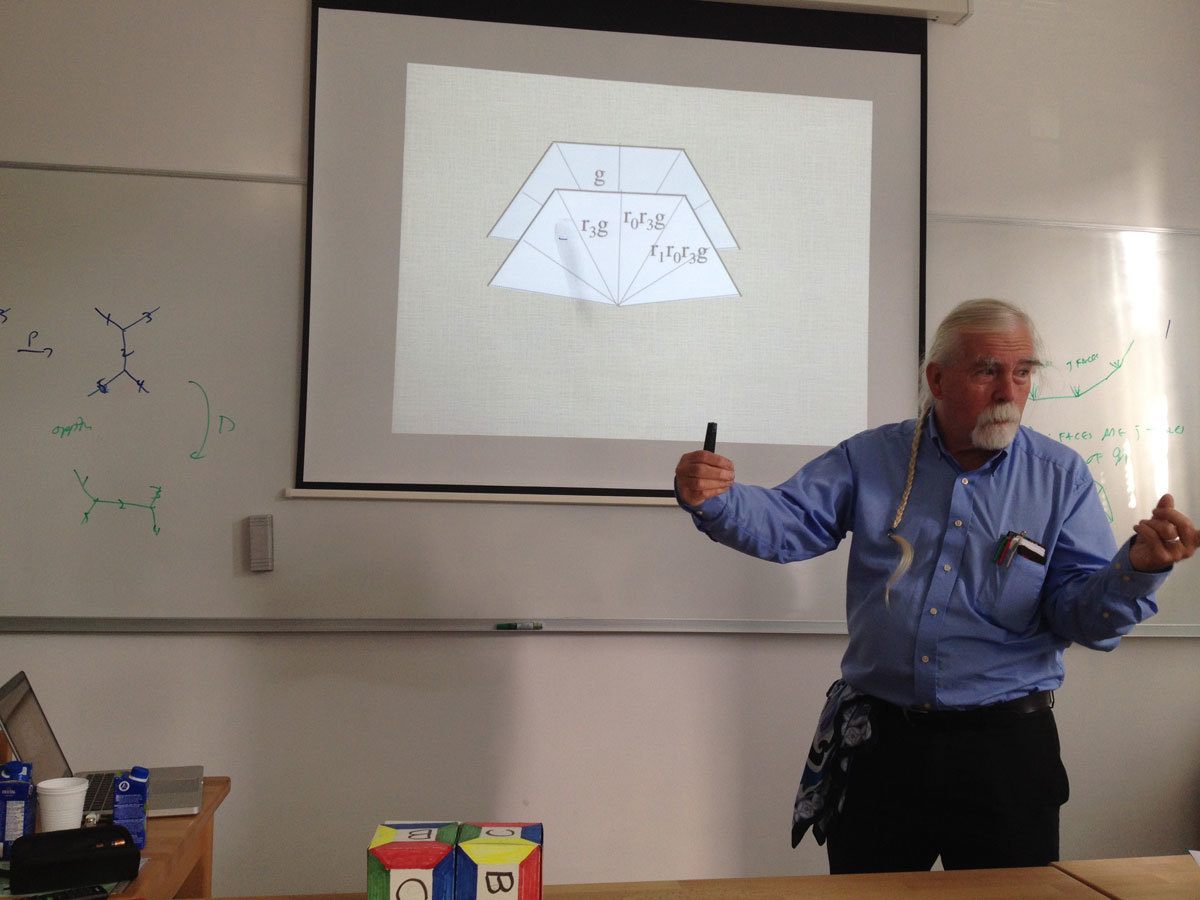
'Maniplex' is a generalization of 'polytope' and is at the same time a generalization of 'map'.  We are interested in those which have large symmetry groups, and these come in two kinds, 'rotary' and 'reflexible', both called 'regular' by some faction of the community.  In this talk, we will introduce manilexes, talk about the motivations for the definition, give some basic examples of several dimensions, and discuss the distinction between maniplexes and polytopes.  Our main goal is to understand a handful of operators (Dual, Petrie, Bubble, Twist) which transform one regular maniplex into another.

fa