
Raziskovalni matematični seminar - Arhiv
| 2026 | 2025 | 2024 | 2023 | 2022 | 2021 | 2020 | 2019 | 2018 | 2017 | 2016 | 2015 | 2014 | 2013 | 2012 | 2011 | 2010 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Nim is an impartial game in which two players take turns choosing a pile and removing a positive tokens from it, with the player making the last move winning. Impartial games are solved by finding which positions are winning and losing, the winning move makes your winning position into a losing position for the opponent. A generalization of winning and losing positions is called the Sprague-Grundy function which partitions positions even further and is needed to know how to play the sum of games. Hypergraph Nim is a new generalization of the game Nim in which instead of a single pile we chose multiple, with our choice of piles denoted by a hypergraph. In this talk we will take a look at the Sprague-Grundy function of Hypergraph Nim.

In earlier work with John Shareshian, we asked whether for every number n, there are primes p and r so that every nontrivial binomial coefficient n choose k is divisible by at least one of the two primes. The motivation for the question is from group theory: the question is equivalent to that of whether for every n there are primes p,r so that the alternating group A_n is generated by any Sylow subgroups at p and r. The answer is "yes" up to a set of asymptotic density zero (assuming the Riemann Hypothesis), and we verified a "yes" answer computationally out to 1 billion.
In more recent work, joined by Bob Guralnick, we have verified computationally that a stronger condition holds for all n out to 7 billion. This computation finishes in a few hours, which is a great improvement over the 2 weeks that our earlier computation out to 1 billion took.
In this talk, I'll overview the interplay between group theory, number theory, and computation allowing this computation.


If we let n(k, d) denote the order of the largest undirected graphs of maximum degree k and diameter d, and let M(k,d) denote the corresponding Moore bound, then n(k,d)\leq M(k,d), for all k\geq 3, d\geq 2. Whilethe inequality has been proved strict for all but very few pairs k and d, the exact relation between the values n(k,d) and M(k,d) is unknown, and the uncertainty of the situation is captured by an open question of Bermond and Bollobas who asked whether it is true that for any positive integer c>0 there exist a pair k and d, such that n(k,d)\leq M(k,d)-c.
In this talk we present a connection of this question to the value 2\sqrt{k-1}, which is also essential in the definition of the Ramanujan graphs defined as k-regular graphs whose second largest eigenvalue (in modulus) does not exceed 2\sqrt{k-1}. We further reinforce this surprising connection by showing that if the answer to the question of Bermond and Bollobas were negative and there existed a c > 0 such that n(k,d) \geq M(k,d) - c, for all k\geq 3, d\geq 2, then, for any fixed k and all sufficiently large even d's, the largest undirected graphs of degree k and diameter d would have to be Ramanujan graphs. This would imply a positive answer to the open question whether infinitely many non-bipartite k-regular Ramanujan graphs exist for any degree k.

In this talk, we consider secondary construction methods of bent and plateaued functions.
The first part of this talk focuses on plateaued functions, where we analyse the concept of its dual. In contrary to bent functions, for which the dual is well established, the dual of a plateaued functions never received enough attention. Using suitable ordering(s) in combination with signs of non-zero entries of the Walsh spectra of a plateaued function, we show that new characterization of plateaued functions can be derived. In addition, these results will lead to completely new approach (so-called Spectral method) for construction of cryptographically significant Boolean functions.
The second part of the talk focuses on secondary constructions of bent and plateaued functions. As we noticed that almost all secondary constructions deduced in the last four decades can be generalized using the composition of one Boolean (usually plateaued) and one vectorial function, we show how one can generalize almost all known secondary construction methods of bent and plateaued functions, by applying the concept of the dual developed for plateaued functions. The so-called “composite representation” of Boolean functions gives a better understanding of the existing secondary constructions and it also allows us to provide a general construction framework of these objects.

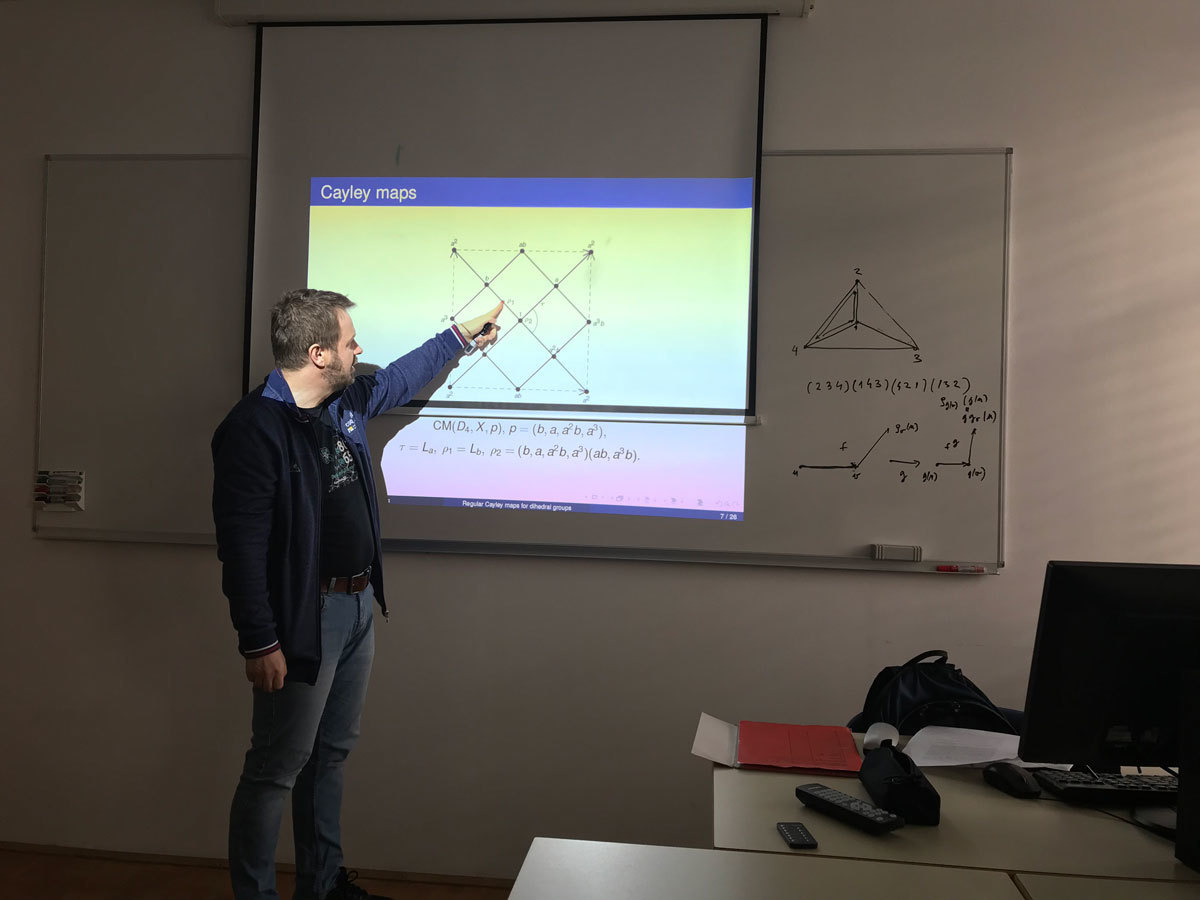
A combinatorial map is a pair M=(X,r), where X is a finite simple connected graph and r is a permutation of its arcs (directed edges) such that the orbit of the arc (u,v) under r is the set of arcs emanating from u. Aut(M) consists of the automorphisms of X for which the induced permutations on the arcs commute with r. The order |Aut(M)| is less than equal to 2|E(G)|, and when equality holds M is called regular. M is a Cayley map for a finite group G if X=Cay(G,S), and r is defined by (h,g) -> (h,p(h^{-1}g)), where h^{-1} \in S and p is a fixed cyclic permutation of S. Regular Cayley maps for cyclic groups were classified by Conder and Tucker (Trans. Amer. Math. Soc., 2014). In this talk, I will show the classification of regular Cayley maps for dihedral groups.

The talk provides a brief introduction to routing games and related game theory concepts. We will discuss different variants and simple examples.
In the second part of the talk, we will look at a dynamic routing game with a special forwarding policy in which a player's priority depends on the previous edge of the chosen path. We present properties and efficiency of equilibria and we specify an algorithm for their calculation. Finally, we give some additional results and open problems.











