Raziskovalni matematični seminar - Arhiv
| 2026 | 2025 | 2024 | 2023 | 2022 | 2021 | 2020 | 2019 | 2018 | 2017 | 2016 | 2015 | 2014 | 2013 | 2012 | 2011 | 2010 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
The subgroup lattice of a group G is the poset consisting of the subgroups of G, ordered by inclusion. Can you recognize whether a group is in a class from its subgroup lattice? For some nice families of groups such as abelian, Hamiltonian, or nilpotent, the answer is "no"; while for other classes such as supersolvable or solvable, the answer is "yes". I'll give several conditions on a subgroup lattice that are equivalent to solvability of the originating group: combinatorial, topological, and commutative algebraic.




Frucht (1939) proved that every abstract finite group is isomorphic to the automorphism group of some finite graph. Jordan (1869) studied automorphism groups of trees. Babai (1991) gives an elegant inductive description of the automorphism groups of trees as the class of groups of closed under direct products and wreath products with symmetric groups. We call similar inductive characterizations of possible automorphism groups as Jordan-like.
We describe Jordan-like characterizations of the automorphism groups of several geometrically represented graph classes including planar, interval, permutation, and circle graphs. These characterizations are based on a general technique in which an automorphism group is studied by its induced action on the set of all geometric representations: each automorphism is either an automorphism of a representation, or a morphism of one representation into another one. When the structure of all representations is well understood (for instance, captured by a suitable tree decomposition) and the action is faithful enough, we can deduce the automorphism groups.
In my talk, I will illustrate this technique on the most complicated case of planar graphs. Babai (1975) characterized which abstract groups can be realized as the automorphism groups of planar graphs. We describe the first inductive Jordan-like characterization of these groups. We use the augmented 3-connected decomposition which divides a graph into its 3-connected components while capturing its symmetries, developed for our previous study of regular graph covers of planar graphs. The Jordan-like characterization first describes the stabilizers of vertices in connected planar graphs as the class of groups closed under the direct and semidirect products with symmetric, dihedral and cyclic groups. The automorphism group of a connected planar graph is then obtained as a semidirect product of a direct product of these stabilizers with a spherical group.
(joint work with Roman Nedela and Peter Zeman)
Lattices appear throughout mathematics: from logics and set theory, to algebra (congruence lattice and lattice of subvarieties), discrete mathematics (face lattice of a polytope and matroids) and topology. Noncommutative lattices can be studied either as generalizations of lattices or as double semigroups of idempotents. We shall describe both approaches and present results that reveal an interesting geometrical structure that allows several combinatorial observations.




Let \F_q be a finite field with q elements, where q is odd, and let A=A^{\top}\in GL_n(\F_q) be an invertible symmetric matrix of size n with coefficients in \F_q. The talk will be about the maps \Phi :\F_q^n\to \F_q^n that satisfy the implication
(x-y)^{\top}A(x-y)=0, x\neq y
\Longrightarrow
\big(\Phi(x)-\Phi(y)\big)^{\top}A\big(\Phi(x)-\Phi(y)\big)=0, \Phi(x)\neq \Phi(y)
for all column vectors x,y\in \F_q^n. The classification problem of such maps is partially related to some physics. The results and the techniques applied in the proofs are related to finite geometry and graph theory. Primarily, this is a typical `preserver problem' studied in matrix theory.

The electrical activity generated by nerve cells of the brain can be measured through electrodes attached to various locations on the scalp. This technique is known as electroencephalography (EEG) and is helpful not only in clinical work, but also in studying various cognitive processes. In the talk we present how graph theory can be used to analyse EEG data. The efficiency of the graph-theoretical approach is illustrated in the case of a mild cognitive impairment.




Properties of fullerenes are critically dependent on the distribution of their 12 pentagonal faces. It is well known that there are infinitely many IPR-fullerenes. IPR-fullerenes can be described as fullerenes in which each connected cluster of pentagons has size 1.
We studied the combinations of cluster sizes that can occur in fullerenes (and whether the clusters can be at an arbitrarily large distance from each other). For each possible partition of the number 12, we are able to decide whether the partition describes the sizes of pentagon clusters in a possible fullerene.
This is joint work with Gunnar Brinkmann, Patrick W. Fowler, Tomaž Pisanski and Nico Van Cleemput.




We shall recall of basic principles of the non-commutative harmonic analysis, discuss the case of classical groups, and how problems of non-commutative harmonic analysis in this case are linked with some important problems of modern theory of automorphic forms.



In our talk, a highly symmetric graph will mean a vertex-transitive graph whose automorphism group is much larger than the order of the graph. We will introduce two numerical parameters - the Cayley and quasi-Cayley deficiency - that will allow us to divide the class of highly symmetric graphs into disjoint subfamilies. We will discuss several known families of highly symmetric graphs, determine their Cayley and quasi-Cayley deficiencies, and try to ask the question which graphs are extremal with regard to these parameters.




Kahler manifolds appear naturally in both Algebraic and Differential Geometry: projective complex varieties from Algebraic Geometry, and smooth manifolds with riemannian metrics with holonomy U(n). Understanding when a manifold may admit a Kahler structure and how far it is from that is a key problem in geometry. Classically, tools from global analysis (harmonic forms and Hodge theory) provide striking topological properties of Kahler manifolds, linking topology and analysis. We shall review this circle of ideas, and recent results on the construction of manifolds admitting complex structures (and even both complex and symplectic structures simultaenously) but not admitting Kahler structures.


The research field of Inverse Problems has witnessed a tremendous growth in recent years, due to its ability to capture and tackle complex problems occuring in real-world applications. However, numerous inverse problems are ill-posed.
Depending on the nature of the problem, various approaches can be considered for stable approximation of the solution. This talk discusses variational and iterative regularization approaches, with emphasis on reconstructing nonnegative solutions when nonnegative data are available.




For positive integers n \ge 2k, the Kneser graph KG(n, k) has as vertices the k-subsets of [n] = {1,...,n} and two vertices are connected by an edge if they have empty intersection. In particular, for s \ge 2, the s-stable Kneser graph is the subgraph of KG(n, k) induced by the k-subsets S of [n] such that the circular distance between any two elements in S is at least s. For this graph class there are several open problems, among them the hom-idempotence and finding its chromatic number. Some papers solve these problems in particular instances, but the general case remains open. In this talk we show some conjectures and advances on them.
SLIDES from the talk are here.




In 1955 Gerhard Ringel introduced the notion of Hamilton Surface Decomposition. 30 years later he wrote two more papers with Nora Hartsfield and Brad Jackson on the same topic. Approximately at the same time I wrote a manuscript together with Brian Alspach. Our result generalizes a lot Ringel’s original result. About 30 years we were polishing the paper, even with help of Alen Orbanić. The purpose of this talk is to test whether the paper is ready to be published.




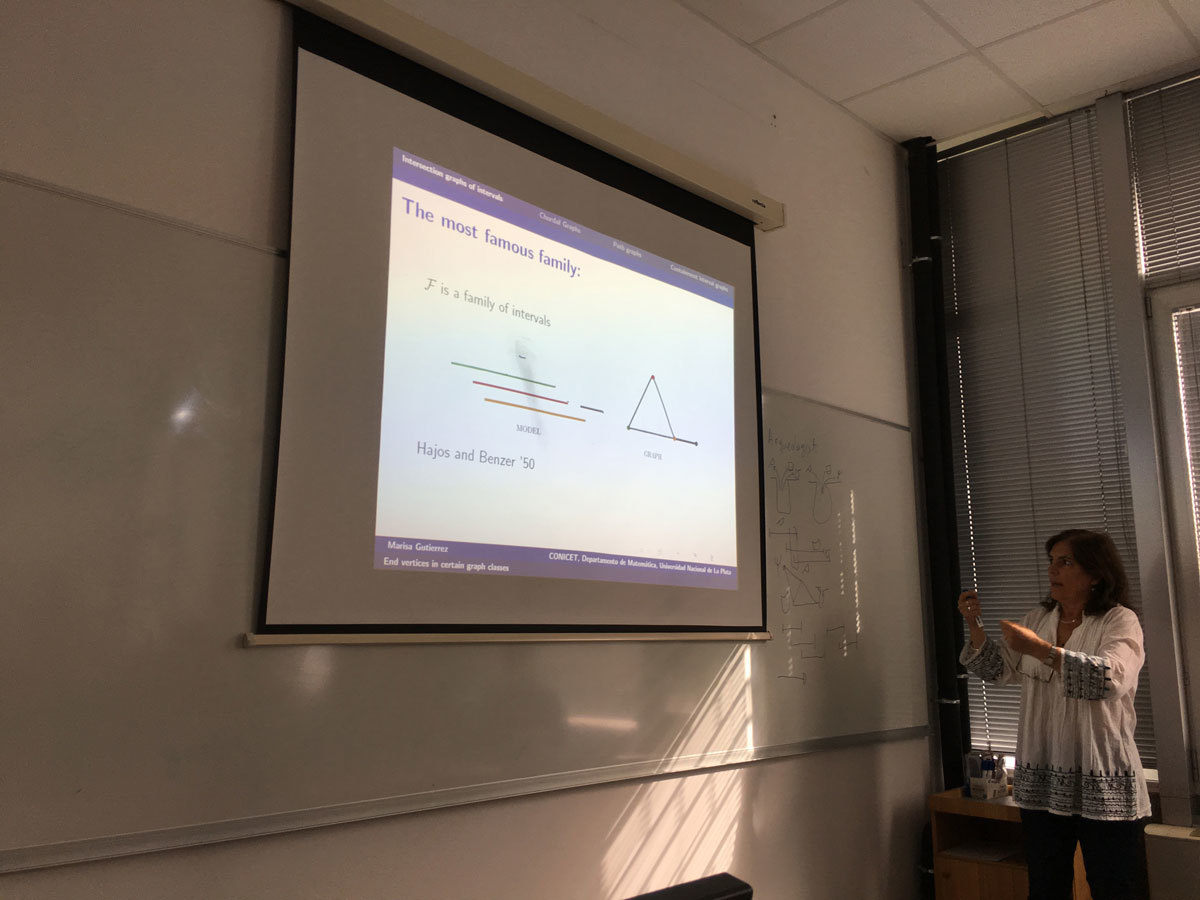
Given a finite family of non empty sets F =(A_i)_{i\in I} it is possible define two graphs associated with the family: the intersection graph of F with set of vertices I and such that two vertices i, j are adjacent if and only if A_i∩A_j \ne \emptyset; and the containment graph of F in which I is also the vertex set but two vertices i, j are adjacent if and only if A_i ⊂ Aj or Aj ⊂ Ai. In both cases F is a model of G.
Different classes of graphs can be defined by considering special classes of sets. For example interval graphs are the intersection graphs of intervals of the real line. The path graphs are the intersection graphs of paths in a tree. These graphs have aroused great attention because storing and accessing the structured information of a graph can be made more efficiently if this is the graph of Intersection of families with good properties [2]. On the other hand, the CI graphs that are the containment graphs of intervals of the real line are studied.
In any case it is natural ask which are the vertices of the graph that can be end vertices in the model? An end vertex v of an interval graph is one such that there is a model of the graph such that Av is more to the left in the model. Gimbel [1] totally characterizes these vertices given forbidden vertices in a family of graphs.
In this work we give these kind of characterizations for leaves vertices in the path graphs [3] and end vertices in containment graphs [4].
Bibliography:
[1] J. Gimbel, End vertices in interval graphs, Discrete Applied Mathematics 21 (1988) 257-259.
[2] J.Spinrad, Efficient Graph Representations, American Mathematical Society (2003) USA.
[3] M. Gutierrez and S. Tondato, End simplicial vertices in path graphs. Discussions Mathematicae Graph Theory. In press (2016).
[4] L. Alcon, N. Gudino and M. Gutierrez, End vertices in containment interval graphs. In process.

Jigsaw percolation is a model for collaborative problem solving: a nonlocal process that iteratively merges connected clusters in a puzzle graph by using connectivity properties of people graph on the same set of vertices. We presume the people graph is random while the puzzle graph is a fixed deterministic graph. The main question is to estimate the probability that the puzzle is solved, that is, that the process eventually produces a single cluster. Particularly sharp answers can be obtained for the one dimensional ring puzzle.
The talk is on joint work with David Sivakoff.




The notion of bounded expansion has been introduced by Nešetřil and Ossona de Mendez as a general concept of sparsity. Classes of graphs of bounded expansion are interesting as they generalize many known sparse classes (as planar graphs, graphs of bounded degree, graphs excluding a minor, etc.). Moreover, several algorithmic problems that are known to be computationally hard in general turn out to be solvable in polynomial time when the inputs are taken in a class of bounded expansion fixed in advance.
On the other hand, classes of graphs with (balanced) sublinear separators are extensively used in the design of algorithms (with "Divide and Conquer" type techniques for instance) and enjoy nice structural properties. An example of graphs with sublinear separators is the class of planar graphs, by a classic result of Lipton and Tarjan.
The topic of this talk is the links between these two notions. Let C be a subgraph-closed class of graphs. Dvořák and Norin proved that graphs in C have sublinear balanced separators iff they have polynomial expansion. They conjectured that if the balanced separators in C have size O(n^{1−δ}) (for some 0 < δ ≤ 1), then the expansion in C is O(k^{c/δ}), for some constant c. We prove this conjecture. This is joint work with Louis Esperet.
This is a presentation of the PhD thesis topic.
Let \G denote a bipartite distance-regular graph with diameter D \ge 4 and valency k \ge 3. Let X denote the vertex set of \G, and let A denote the adjacency matrix of \G. For x \in X and for 0 \le i \le D, let \G_i(x) denote the set of vertices in X that are distance i from vertex x. Define parameters \Delta_i (1\le i\le D-1) in terms of the intersection numbers by \Delta_i=(b_{i-1} - 1)(c_{i+1} - 1) - (c_2 - 1)p^i_{2i}. In PhD thesis we show that \Delta_2 = 0 implies D \le 5 or c_2 \in \{1,2\}.
For x \in X let T=T(x) denote the subalgebra of \MX generated by A, \Es_0, \Es_1, \ldots, \Es_D, where for 0 \le i \le D, \Es_i represents the projection onto the i-th subconstituent of \G with respect to x. We refer to T as the Terwilliger algebra of \G with respect to x. By the endpoint of an irreducible T-module W we mean \min\{i | \Es_iW \ne 0\}.
Consider a bipartite DRG \G with one of the following properties:
(b.1) \G has, up to isomorphism, a unique irreducible T-module W of endpoint 2, this module is not thin, \dim(\Es_iW)\le 2 for every i (2\le i\le D-1) and \dim(\Es_2W)= 1.
(b.2) \Delta_i=0 for every i (2\le i\le D-1).
(b.3) \G has the property that for 2\le i\le D-1, there exist complex scalars \alpha_i, \beta_i such that for all x,y,z\in X with \partial(x,y)=2, \partial(x,z)=i, \partial(y,z)=i, we have \alpha_i+\beta_i|\G_1(x)\cap\G_1(y)\cap\G_{i-1}(z)|=|\G_{i-1}(x)\cap\G_{i-1}(y)\cap\G_{1}(z)|.
(b.4) \Delta_2=0, \Delta_i\not=0 for at least one i (3\le i\le D-2), and (b.3) holds.
In this PhD Thesis we will show that the property (b.4) implies property (b.1). Note that property (b.4) includes (b.3) by definition, and we are interested in bipartite distance-regular graphs with property (b.3) because they arise as a natural family in the study of the Terwilliger algebra of a bipartite distance-regular graph, as we will see by the following very important example. Suppose that \G is Q-polynomial. Then \G has, up to isomorphism, at most one irreducible T-module of endpoint 2 and diameter D-2, at most one irreducible T-module of endpoint 2 and diameter D-4 (they are both thin), and no other irreducible T-modules of endpoint 2, see [J. S. Caughman, IV, The Terwilliger algebras of bipartite P- and Q-polynomial schemes, Discrete Math. 196 (1999), 65--95.]. Furthermore, Terwilliger's {\it balanced set condition} ([P. Terwilliger, A new inequality for distance-regular graphs, Discrete Math. 137 (1995), 319--332.]) implies the property (b.3) ([Š. Miklavič, On bipartite Q-polynomial distance-regular graphs, European J. Combin. 28 (2007), 94--110.]).
In this PhD Thesis, we will not assume the Q-polynomial property for \G, but rather the property (b.3) above, together with \Delta_2=0. It is our goal to describe the irreducible T-modules with endpoint 2 for this case. We assume that \Delta_i\not=0 for at least one i (3\le i\le D-2), since graphs with property (b.2) are already well-understood ([B. Curtin, Almost 2-homogeneous bipartite distance-regular graphs, European J. Combin. 21 (2000), 865--876.]). First we will show that in case when c_2\le 2, there exists a certain equitable partition of the vertex set of \G which, for case c_2=1, involves 3(D-1)+\ell cells and, for case c_2=2, involves 4(D-1)+2\ell cells, for some integer \ell with 0\le\ell\le D-2. We use this equitable partition to describe the irreducible T-modules with endpoint 2 for this case.
In the second part of the thesis we assume \G is a bipartite Q-polynomial distance-regular graph with diameter D \ge 4, valency k \ge 3 and intersection numbers b_i, c_i. Caughman proved in [J. S. Caughman, IV, Bipartite Q-polynomial distance-regular graphs, Graphs Combin. 20 (2004), 47--57.] that if D \ge 12 then \G is either the D-dimensional hypercube, or the antipodal quotient of the 2D-dimensional hypercube, or the intersection numbers of \G satisfy c_i = (q^i-1)/(q-1) \; (0 \le i \le D) for some integer q at least 2. Note that if c_2 \le 2, then the last of the above possibilities cannot occur. The aim of this PhD thesis will also be to further investigate these graphs. We will show that if c_2 \le 2 then \G is either the D-dimensional hypercube, or the antipodal quotient of the 2D-dimensional hypercube, or D=5.
In the problems of (i) finding equitable partition for c_2\le 2; (ii) describing irreducible T-modules with endpoint 2 and (iii) proving that Q-polynomial distance-regular graph \G is either the D-dimensional hypercube, or the antipodal quotient of the 2D-dimensional hypercube, or D=5; we use combinatorial and linear algebra methods similar to those that are used in [Š. Miklavič and S. Penjić, "On bipartite Q-polynomial distance-regular graphs with c_2 ≤ 2", The Electronic Journal of Combinatorics 21(4) (2014), #P4.53.], [M. S. MacLeana, Š. Miklavič, S. Penjić, "On the Terwilliger algebra of bipartite distance-regular graphs with \Delta_2=0 and c_2=1", Linear Algebra and its Applications 496 (2016), 307–330.] and [S. Penjić, "On the Terwilliger algebra of bipartite distance-regular graphs with \Delta_2=0 and c_2=2", Discrete Mathematics 340 (2017), 452–466].
I'll show how to construct a subspace arrangement which encodes the independence polynomial of a graph G. I'll discuss possible applications to unimodality questions.
Povezanost med umetnostjo in znanostjo, še posebej z matematiko, je zgodovinsko dokazana. S pojavom digitalne umetnosti je matematika pridobila še dodatno vlogo, saj se neposredno vključuje v sam proces nastajanja umetniških del. Tudi preprost programski algoritem ne more brez pomoči matematike narisati niti najenostavnejših elementov slike. Moja raziskovanja na področju razvoja programske opreme za generiranje slik so bila zato vedno tesno povezana z iskanjem inovativnih rešitev v okviru poznanih matematičnih principov. V okviru predavanja bom predstavil osnovna izhodišča za risanje slike v ravnini s kartezičnimi in polarnimi koordinatami ter risanje slike v kompleksni ravnini. Poleg nazornega prikaza »vizualizacije« konkretnih matematičnih izrazov bom demonstriral delovanje parih programov, ki uporabljajo opisane koncepte.
e-mail: bogdan@soban-art.com
spletna stran: www.soban-art.com
Two new classes of bent functions derived from the Maiorana-McFarland class, so-called C and D, were introduced by Carlet two decades ago. However, apart from the subclassD_0, some explicit construction methods for these functions were not provided. Assuming the possibility of specifying a bent function f that belongs to one of these two classes (apart from D_0), the most important issue is then to determine whether f is still contained in the known primary classes or lies outside their completed versions. In this article we partially solve this question by providing sufficient conditions on the permutation and related characteristic function so that f is provably outside the completed Maiorana-McFarland class.





Some connections between designs and codes will be discussed. Further, we present the enumeration of quasi-symmetric 2-(64,24,46) designs supported by the dual code C^{\perp} of the binary linear code C spanned by the lines of AG(3,4).




A Hadamard matrix of order m is a (m \times m) matrix H=( h_{i,j}), h_{i,j} \in \{ -1,1 \}, satisfying HH^T=H^TH=mI_m, where I_m is an (m \times m) identity matrix. A Hadamard matrix is called regular if the row and column sums are constant. It is conjectured that a regular Hadamard matrix of order 4k^2 exists for every positive integer k. We will give some method of constructing regular Hadamard matrices and related self-orthogonal codes.




The Moore bound M(k,g) is a lower bound on the order of k-regular graphs of girth g (denoted (k,g)-graphs). The excess e of a (k,g)-graph of order n is the difference n-M(k,g). We consider the existence of (k,g)-bipartite graphs of excess 4 by studying spectral properties of their adjacency matrices.
For a given graph G and for the integers i with 0\leq i\leq diam(G), the i-distance matrix A_i of G is an n\times n matrix such that the entry in position (u,v) is 1 if the distance between the vertices u and v is i, and zero otherwise.
We prove that the (k,g)-bipartite graphs of excess 4 satisfy the equation kJ=(A+kI)(H_{d-1}(A)+E), where A=A_{1} denotes the adjacency matrix of the graph in question, J the n \times n all-ones matrix, E=A_{d+1} the adjacency matrix of a union of vertex-disjoint cycles, and H_{d-1}(x) is the Dickson polynomial of the second kind with parameter k-1 and degree d-1. We observe that the eigenvalues other than \pm k of these graphs are roots of the polynomials H_{d-1}(x)+\lambda, where \lambda is an eigenvalue of E.
Based on the irreducibility of $H_{d-1}(x)\pm2$, we give necessary conditions for the existence of these graphs. If E is the adjacency matrix of a cycle of order n, we call the corresponding graphs {graphs with cyclic excess; if E is the adjacency matrix of a disjoint union of two cycles, we call the corresponding graphs graphs with bicyclic excess. We prove the non-existence of (k,g)-graphs with cyclic excess 4 if k\geq 6 and k \equiv 1 \pmod 3, g=8, 12, 16 or k \equiv 2 \pmod 3, g=8; and the non-existence of (k,g)-graphs with bicyclic excess 4 if k\geq 7 is an odd number and g=2d such that d\geq 4 is even.




Let G be a graph with a proper vertex colouring. Let a and b be two of the colours. Then a connected component of the subgraph induced by those vertices coloured either a or b is known as a Kempe chain. Another proper colouring of G can be obtained by swapping the colours on the vertices of a Kempe chain. This colouring is said to have been obtained by a Kempe change. Two colourings of G are Kempe equivalent if one can be obtained from the other by a sequence of Kempe changes.
Kempe chains were introduced by Alfred Kempe in an attempt to prove the Four Colour Theorem. Though this attempt failed, the method of Kempe chains was used in the proof of the Five Colour Theorem and elsewhere.
We address a 2007 conjecture of Bojan Mohar that asserts that, for k at least 3, all k-colourings of a k-regular graph that is not complete are Kempe equivalent. We show that the conjecture holds with one exception, the triangular prism.
This is joint work with Marthe Bonamy, Nicolas Bousquet, Carl Feghali and Daniel Paulusma.




The Colouring problem is that of deciding, given a graph G and an integer k, whether G admits a (proper) k-colouring. For all graphs H up to five vertices, we classify the computational complexity of Colouring for (diamond,H)-free graphs. Our proof is based on combining known results together with proving that the clique-width is bounded for (diamond,P_1+2P_2)-free graphs. Our technique for handling this case is to reduce the graph under consideration to a k-partite graph that has a very specific decomposition. As a by-product of this general technique we are also able to prove boundedness of clique-width for four other classes of (H1,H2)-free graphs. As such, our work also continues a systematic study into the (un)boundedness of clique-width of (H_1,H_2)-free graphs.
Joint work with Konrad Dabrowski and François Dross.




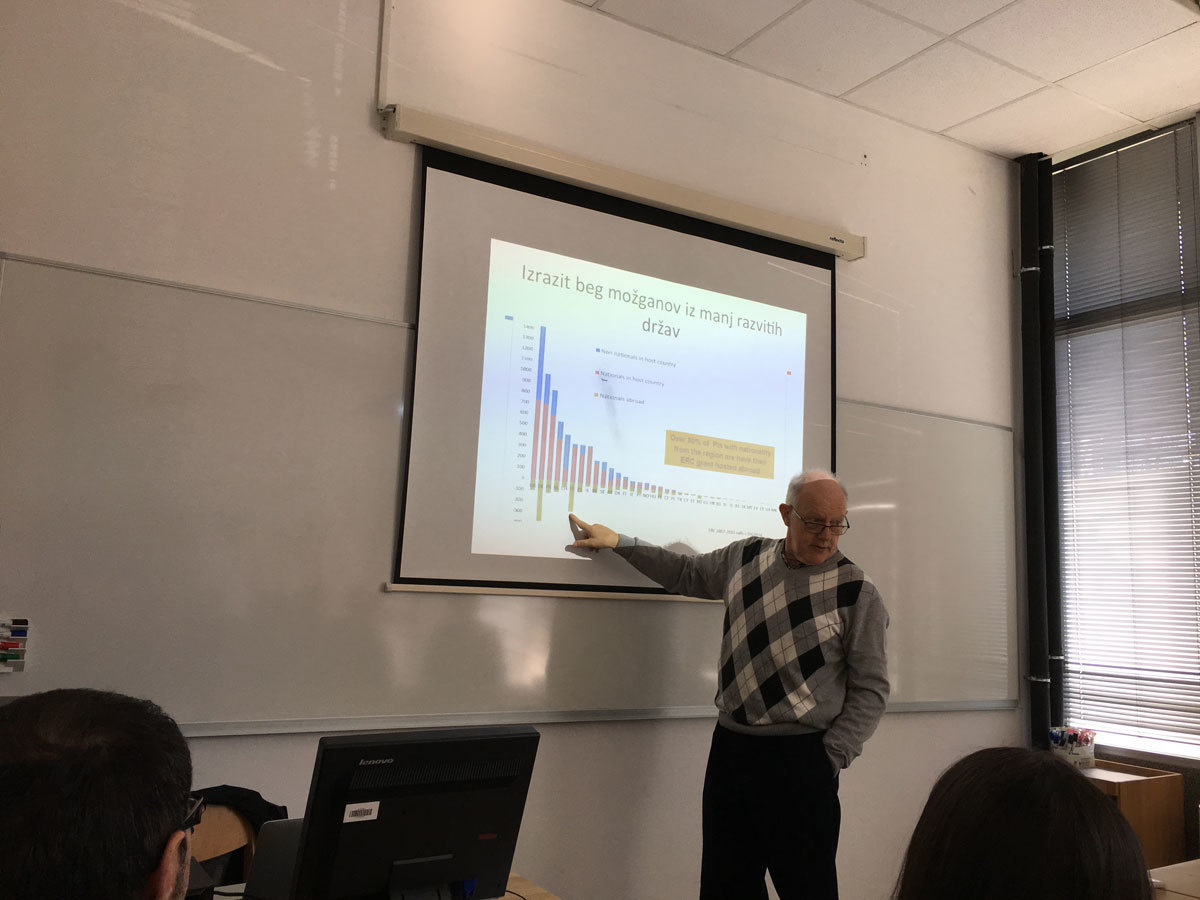
The aim of this talk is to analyze poor performance of Slovenia at the ERC grant calls. In particular, we will present five major errors in the scientific policy in Mathematics in Slovenia over a span of several decades. We will also point out some other reasons for underperformance of Slovenia and other EU13 countries.



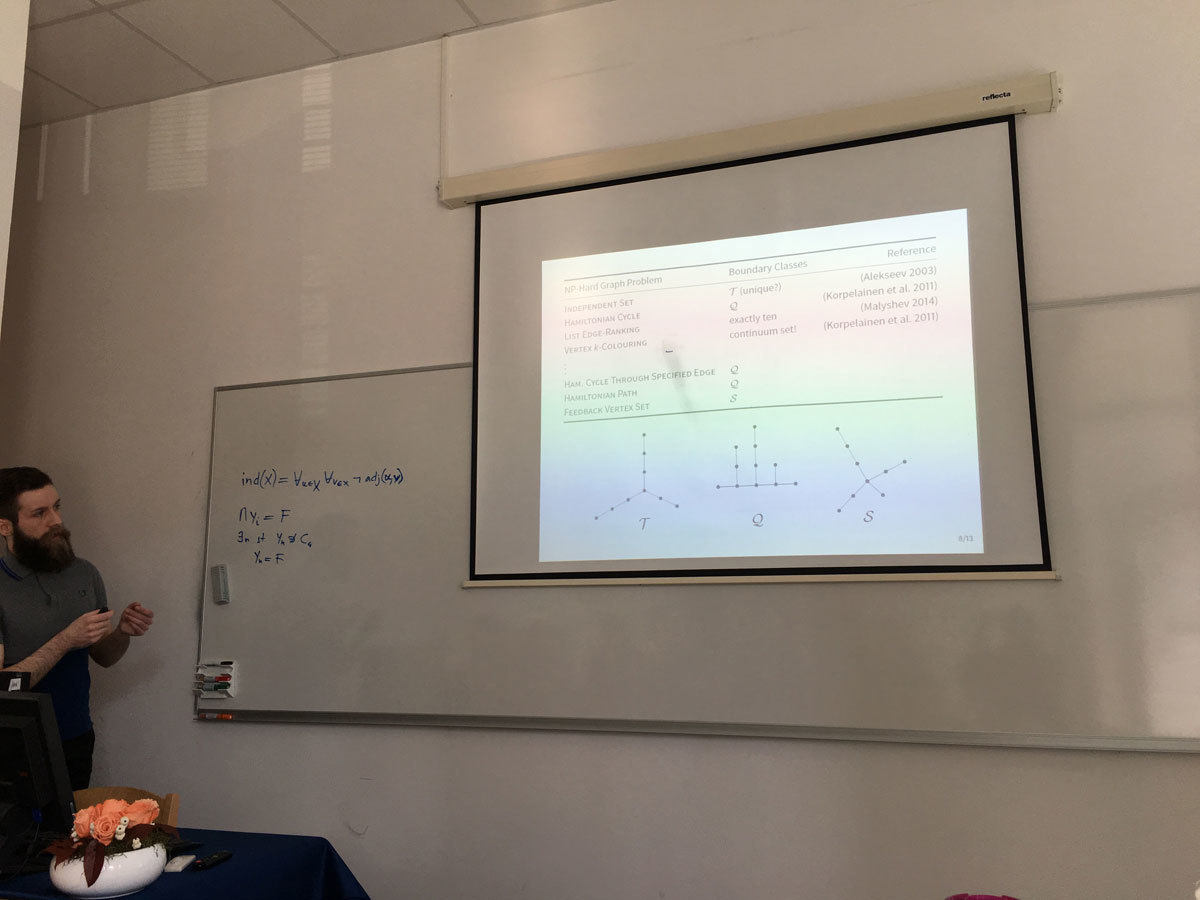
Many NP-hard graph problems remain NP-hard even for restricted classes of graphs, while they become polynomial-time solvable when further restrictions are applied. It is therefore natural to ask when a certain "hard" graph problem becomes "easy": Is there any "boundary" separating "easy" and "hard" instances? Alekseev considered this question in the case the instances are hereditary classes of graphs.
Given a graph problem Pi, a hereditary class of graphs X is Pi-hard if Pi is NP-hard for X, and Pi-easy if Pi is solvable in polynomial time for graphs in X. He introduced the notion of Pi-boundary class, playing the role of the "boundary" separating Pi-hard and Pi-easy instances, and showed that a finitely defined (hereditary) class is Pi-hard if and only if it contains a Pi-boundary class. Moreover, he determined a boundary class for Independent Set, the first result in the systematic study of boundary classes for NP-hard graph problems.
In the talk, I will review some known results and present new boundary classes for some problems involving non-local properties, like Hamiltonian Path and Feedback Vertex Set.



In this talk we adopt the notion of skeletal polytope introduce by Grunbaum in the second half of the 20th Century. A polygon is then a connected 2-valent graph embedded in Euclidean space (no assumption on convexity or planarity), and in general an n-polytope is a collection of (n-1)-polytopes satisfying certain axioms. Such a structure is called chiral if it admits all possible symmetry by abstract rotations, but none by abstract reflections.
Chiral polyhedra (polytopes of rank 3) were found and classified by Schulte only in 2005. Chiral 4-polytopes were claimed not to exist in 2004. This last claim was mistaken. In this talk we present the three chiral 4-polytopes in space.




A group is called 2-genetic if each normal subgroup of the group can be generated by two elements. Let G be a non-abelian 2-genetic group of order p^n for an odd prime p and a positive integer n. In this paper, we investigate connected Cayley digraphs Cay(G, S), and determine their full automorphism groups when Aut(G, S) = {α\in Aut(G) | S^α = S} is a p′-group. With the result, we give the first known half-arc-transitive non-normal Cayley graphs of order an odd prime-power.



We will define and motivate a minor relation in the family of partial cubes. The main topic of the talk will be the forbidden minors characterizations of well established subfamilies. We will present new results on the family of partial cubes that have no forbidden minor isomorphic to a 3-dimensional hypercube minus a vertex. This family plays an important role in understanding bipartite graphs and in establishing a hierarchy among its subfamilies.




We consider a new type of regularity we call edge-girth-regularity. An edge-girth-regular \((v,k,g,\lambda)\)-graph \(G\) is a \(k\)-regular graph of order \(v\) and girth \(g\) in which every edge is contained in \(\lambda\) distinct \(g\)-cycles. This concept is a generalization of the well-known \((v,k,\lambda)\)-edge-regular graphs (that count the number of triangles) and appears in several related problems such as Moore graphs and Cage and Degree/Diameter Problems. All edge- and arc-transitive graphs are edge-girth-regular as well. We derive a number of basic properties of edge-girth-regular graphs, systematically consider cubic and tetravalent graphs from this class, and introduce several constructions that produce infinite families of edge-girth-regular graphs. We also exhibit several surprising connections to regular embeddings of graphs in orientable surfaces.
Joint work with Robert Jajcay and Štefko Miklavič.