
Raziskovalni matematični seminar - Arhiv
| 2026 | 2025 | 2024 | 2023 | 2022 | 2021 | 2020 | 2019 | 2018 | 2017 | 2016 | 2015 | 2014 | 2013 | 2012 | 2011 | 2010 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
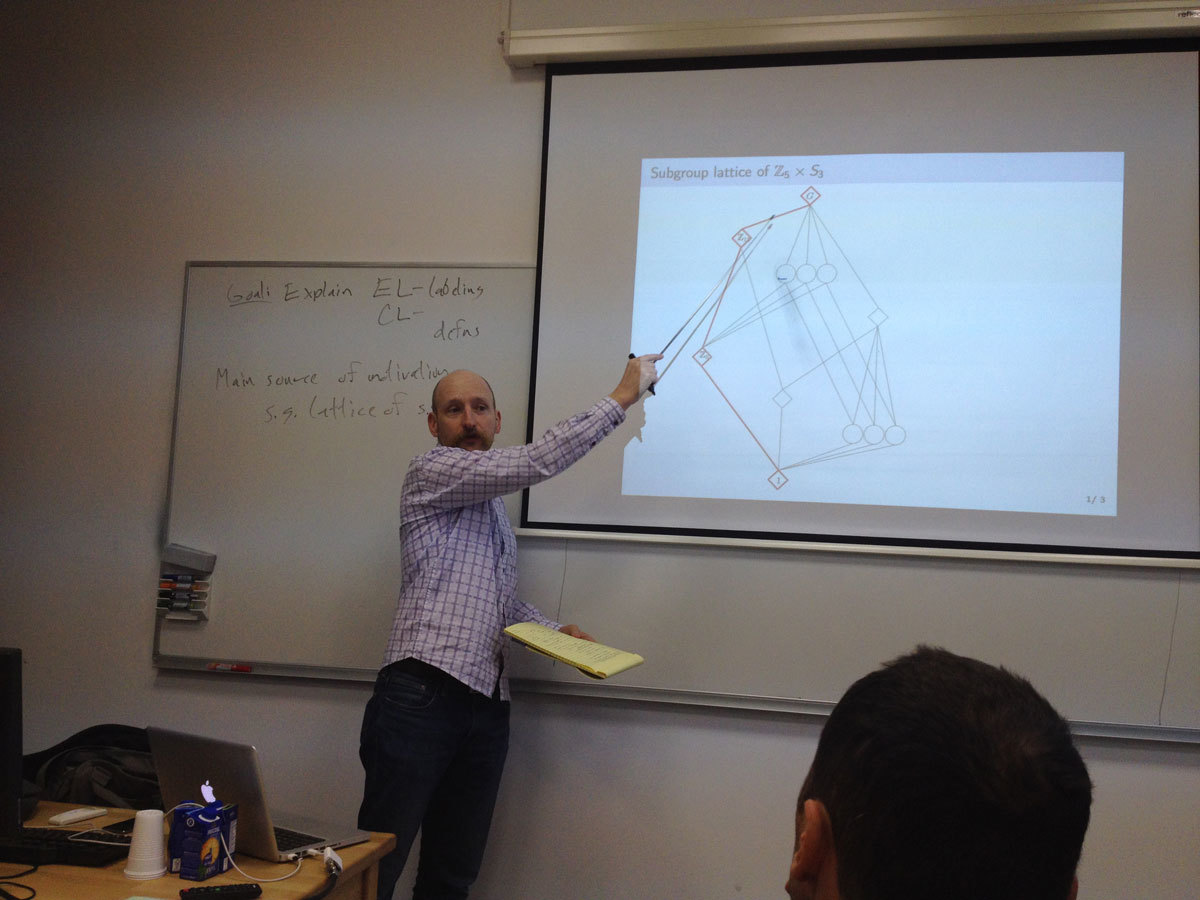
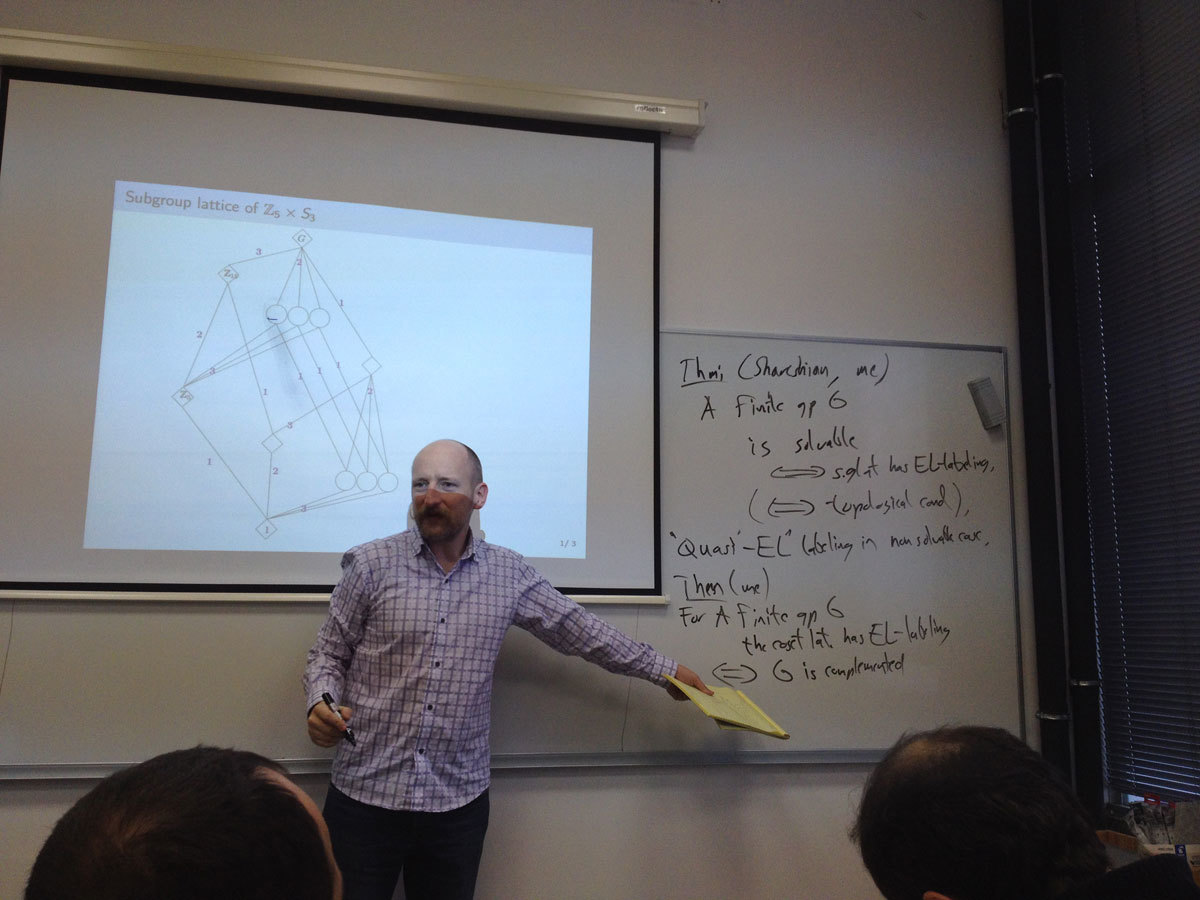
This talk will be about finite lattices and posets. I'll tell you what an EL-labeling is, explain how the subgroup lattice of a supersolvable group motivates its definition, and give related results on lattices defined from groups. Unfortunately, EL-labelings can be difficult to construct, and there are several lattices for which it is not known whether an EL-labeling exists. I'll show how this leads to the idea of a CL-labeling.
My goal, if time allows, is to give a clear idea of recent work of myself and Jay Schweig, in which we show that a certain wide class of lattices has a CL-labeling.




A clique in a graph is said to be strong if it intersects every maximal stable set. A graph is called localizable if it admits a partition of its vertex set into strong cliques. In this talk I will present some results regarding the complexity of recognizing localizable graphs. We will discuss when is the product (lexicographic or Cartesian) of two graphs localizable.
We will also discuss what does it mean for a vertex-transitive graph to have a strong clique.
This is a joint work with Martin Milanič and Bernard Ries.





A Cayley map M=CM(G,X,P) is an embedding of a Cayley graph C(G,X) in an orientable surface with the property that each left multiplication by an element of G becomes a map automorphism of M: G < Aut(M). A Cayley map CM(G,X,P) is regular (i.e., its orientation preserving automorphisms act regularly on darts) if and only if a skew-morphism exists that has an orbit X on which it is equal to P.
With Roman Nedela we asked the question whether the skew-morphisms which do not have this property are good for anything, and arrived at the concept of a half-regular Cayley map.





Let $GF(q)$ denote the finite field with $q$ elements, and let $S$ denote the set of all square elements of $GF(q)$. The norm $N$ of a point $x=(x_1,\ldots,x_n)$ of the affine space $AG(n,q)$ is defined by $N(x) = x_1^2+\cdots+x_n^2,$ and two points $x$ and $y$ are said to be at integral distance if $N(x-y)$ is in $S$. An integral automorphism of $AG(n,q)$ is a permutation of the point set which preserves integral distances. In this talk I present some recent results on integral automorphisms. The talk is based on a joint work with Klavdija Kutnar, J\'anos Ruff and Tam\'as Sz\H onyi.





Abstract: A family F of automorphisms of a vertex-transitive graph G is said to be k-regular if for every pair u,v of vertices of G there exist k automorphisms in F mapping u to v. Every vertex-transitive graph admits a k-regular family for some positive k, and quasi-Cayley graphs are vertex-transitive graphs admitting a 1-regular family of automorphisms. We investigate the class of merged Johnson graphs with regard to the parameter k, classify merged Johnson graphs that are Cayley, and relate this topic to that of the existence of a uniform routing.





In this talk we will give an overview of various aspects of submodular set functions. Several examples of submodular functions will be presented, including modular functions, polymatroid functions, and objective functions of various optimization problems, for example those related to facility location problems and to cuts in graphs.
The problem of minimization and maximization of submodular functions, and the submodular set cover problem will be discussed. Two approximation algorithms will be described: one for the problem of maximizing a given submodular function under a cardinality constraint due to Nemauser et al. and one for the unconstrained submodular maximization due to Buchbinder et al. More precisely, we will present a greedy algorithm for maximizing a submodular function under a cardinality constraint, one deterministic algorithm and two randomized algorithms with approximation factors 1/3, 1/4 and 1/2, respectively, for solving the uncostrained submodular maximization problem.
Finally, a new proof of the theorem due to Boros et al. stating that every hypergraph has an exact polymatroid separator will be given.




A hypergraph is a pair (V,E) such that V is a finite set and E is a set of subsets of V (members of E are called hyperedges). We introduce a new class of hypergraphs, the class of 1-Sperner hypergraphs. A hypergraph H is said to be 1-Sperner if every two distinct hyperedges e,f of H satisfy min { | e \ f | ,| f \ e | } = 1.
We prove a decomposition theorem for 1-Sperner hypergraphs and examine several of its consequences, including bounds on the size of 1-Sperner hypergraphs and a new, constructive proof of the fact that every 1-Sperner hypergraph is threshold. (A hypergraph H = (V,E) is said to be threshold if there exist a non-negative vertex weight function w and a non-negative threshold t such that for every subset X of V, we have w(X) >= t if and only if X contains a hyperedge.)
A hypergraph is said to be Sperner (or: a clutter) if no hyperedge is contained in another one. Given a graph G, the clique hypergraph of G is the hypergraph C(G) with vertex set V(G) in which the hyperedges are exactly the maximal cliques of G. The clique hypergraphs of graphs are known to be exactly those Sperner hypergraphs H that are also normal (or: conformal), that is, for every subset X of V(H) such that every pair of elements in X is contained in a hyperedge, there exists a hyperedge containing X.
We show that within the class of normal Sperner hypergraphs, the (generally properly nested) classes of 1-Sperner hypergraphs, of threshold hypergraphs, and of 2-asummable hypergraphs coincide. This yields new characterizations of the class of threshold graphs.
The talk is based on joint work with Endre Boros and Vladimir Gurvich (both at Rutgers University).
Preprint is available at: http://arxiv.org/abs/1510.02438
Slides of talk are here.





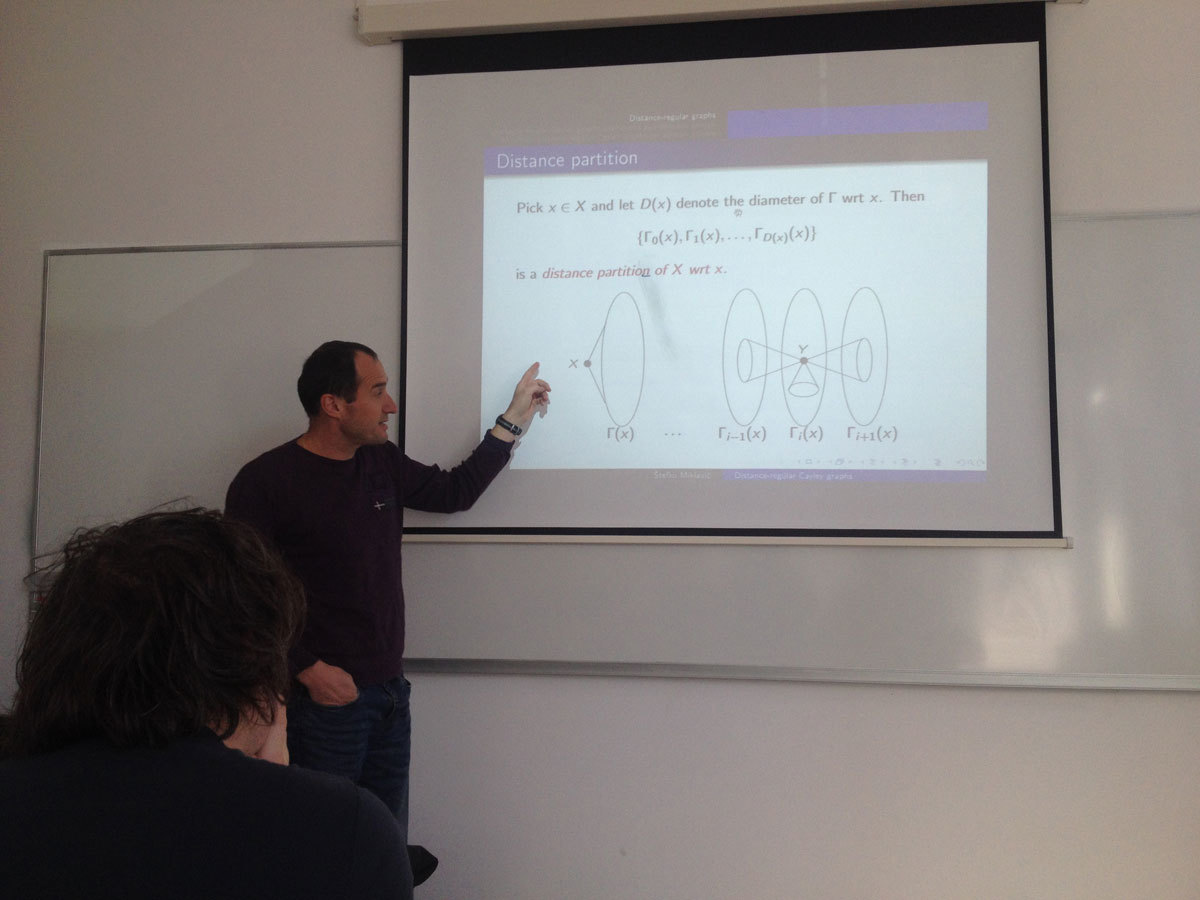
In this talk we consider the following problem: for a given class of groups ${\cal G}$, classify distance-regular Cayley graphs $Cay(G;S)$, where $G \in {\cal G}$.




In a graph, a set of vertices that is stabilized setwise by only the trivial automorphism is called a distinguishing set. Tom Tucker conjectured that every connected, infinite locally finite graph G has such a set if each nontrivial automorphism of G moves infinitely many vertices. The conjecture is know as the Infinite Motion Conjecture, which is still open despite the fact that numerous large classes of graphs have been shown to satisfy it.
In finite graphs distinguishing sets, if they exist, can be very small in comparison to the size of the graph, and in infinite graphs such sets can be finite. If they are not finite, their density can be zero.
This talk introduces to the subject and presents new results about the density of distinguishing sets and the Infinite Motion Conjecture.



In this talk I give necessary and sufficient conditions for when a system of nonlinear delay equations can be reduced to a system of ordinary differential equations. The class of systems considered contains nonlinear models of physiologically structured populations.
My talk is based on joint work (in progress) with Odo Diekmann and Hans Metz.




An automorphism (or symmetry) of a combinatorial graph may be called even or odd according to whether it acts as an even or odd permutation on the vertices of the graph. In this talk, I will present a partial result about the following question: When does the existence of even automorphisms of a graph force existence of odd automorphisms? In particular, I will present complete information the on existence of odd automorphisms for cubic symmetric graphs.




'Maniplex' is a generalization of 'polytope' and is at the same time a generalization of 'map'. We are interested in those which have large symmetry groups, and these come in two kinds, 'rotary' and 'reflexible', both called 'regular' by some faction of the community. In this talk, we will introduce manilexes, talk about the motivations for the definition, give some basic examples of several dimensions, and discuss the distinction between maniplexes and polytopes. Our main goal is to understand a handful of operators (Dual, Petrie, Bubble, Twist) which transform one regular maniplex into another.
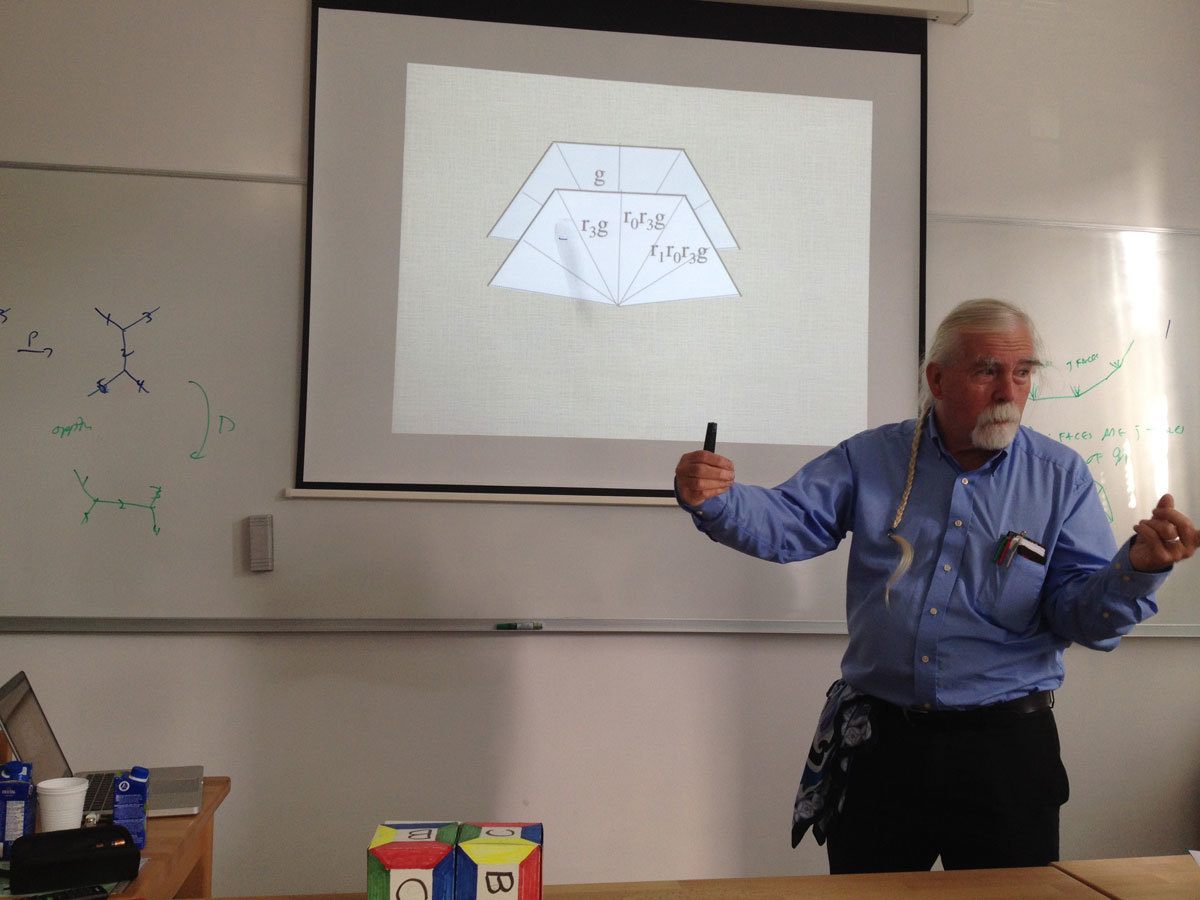


'Maniplex' is a generalization of 'polytope' and is at the same time a generalization of 'map'. We are interested in those which have large symmetry groups, and these come in two kinds, 'rotary' and 'reflexible', both called 'regular' by some faction of the community. In this talk, we will introduce manilexes, talk about the motivations for the definition, give some basic examples of several dimensions, and discuss the distinction between maniplexes and polytopes. Our main goal is to understand a handful of operators (Dual, Petrie, Bubble, Twist) which transform one regular maniplex into another.
 fa
fa


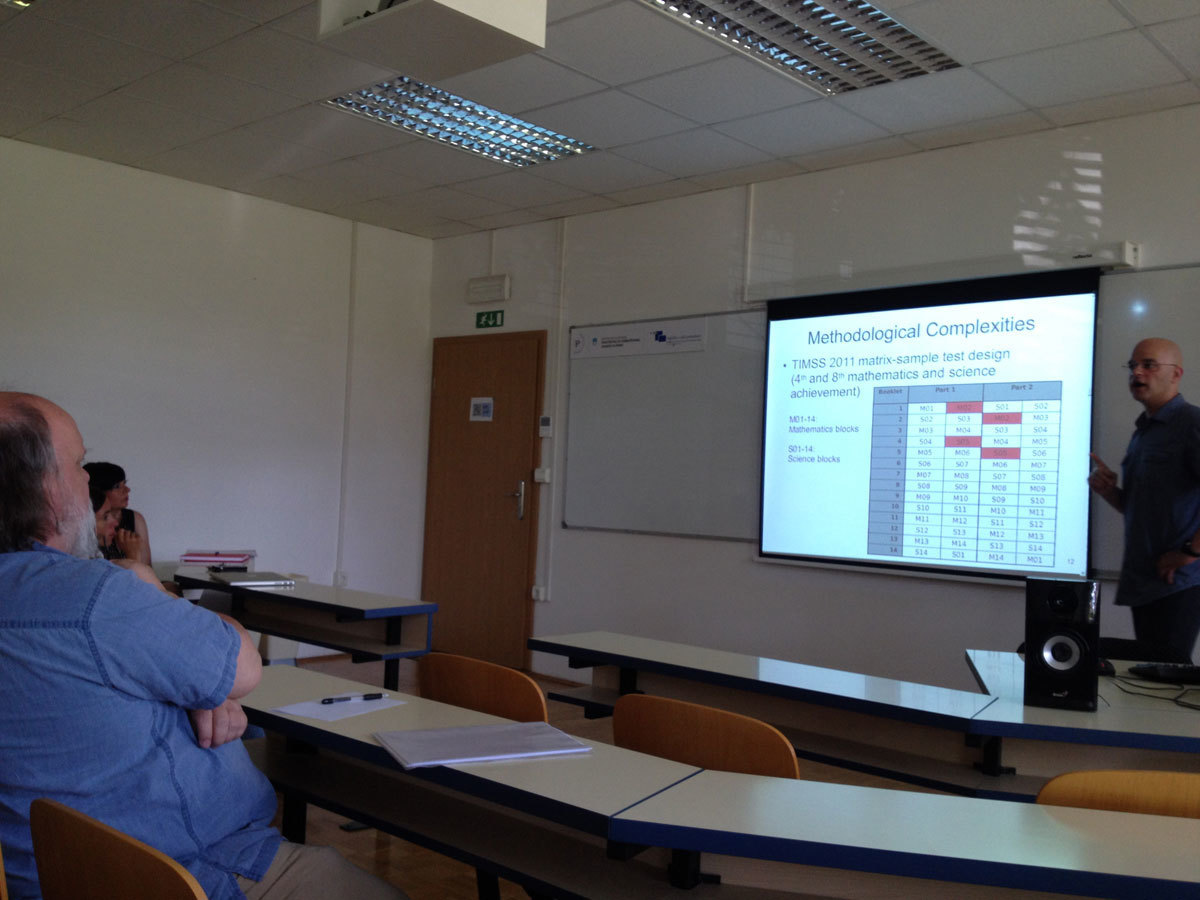
The international large-scale student assessments (ILSA) are on the scene of educational research for more than 50 years. Their role in policy-making in education as drivers for social change becomes more and more important over the last two decades. This presentation will provide an overview of the use of ILSA data for national policy-making in education and reforms' implementation. The presentation will also provide a review of the theoretical and methodological assessment strategies for evaluation of the outcomes of education and their operational, methodological and psychometric complexities arising from the complex sampling and assessment designs. The issues stemming from these complex sample and assessment designs and their implications for analysis and interpretation of the results will be discussed. Limitations to the use of analysis techniques related with the data will be presented as well.




We formulate a massively general framework for optimal dynamic stochastic control problems which allows for a control-dependent informational structure. The issue of informational consistency is brought to light and investigated. Bellman's principle is formulated and proved. In a series of related results, we expound on the informational structure in the context of (completed) natural filtrations of (stochastic) processes.




The topic of our talk is a refinement of the classical result of Frucht, who has shown that for any finite group G, there exists a graph whose full automorphism group is isomorphic to G. Instead of seeking a graph whose automorphism group is isomorphic to G, we choose a specific permutation representation of G on a set V, and ask about the existence of a combinatorial structure on V whose full automorphism group is equal to G in its particular representation. If the permutation representation considered is the regular permutation representation and the combinatorial structures we consider are graphs, the question becomes the well-known questions of which finite groups are the full automorphism groups of some Cayley graph (in case of existence, such Cayley graph is called a Graphical Regular Representation for G). In our talk, we extend the question of regular representations to other classes of combinatorial structures such as incidence structures, directed graphs, designs, maps, or hypergraphs. Our presentation is based on a collaboration with Tatiana Jajcayova.



A Hamiltonian cycle system of odd (even) order v, briefly a HCS(v), is a decomposition of the complete graph Kv (the complete graph Kv minus a 1-factor) into Hamiltonian cycles. I will survey known results and open problems about the automorphism groups of a HCS(v).





We will discuss the problem of describing the general form of adjacency and coherency preservers on 2 by 2 hermitian matrices. This is an elementary problem that can be easily explained to the first year undergraduate students of mathematics. I hope I will succeed to show that such a simple question can generate some interesting mathematics connecting linear algebra, functional analysis, geometry, algebraic topology, and mathematical physics.





Competitive equilibrium problems are usually studied by means of fixed point theory. Alternatively, it is possible to study these problems by means of a variational approach. The variational inequality theory was introduced by Fichera and Stampacchia, in the early 1960's, in connection with several equilibrium problems originating from mathematical physics. This theory turned out to be an innovative and powerful methodology for the study of several kind of equilibrium problems.
Here we consider a new formulation of a competitive equilibrium in terms of a suitable quasivariational inequality involving multivalued maps. More precisely, it is considered a pure exchange economy where the consumer's preferences are represented by quasiconcave and non-differentiable utility functions. By relaxing concavity and differentiability assumptions on the utility functions, the subdifferential operator of the utility function, required in the variational problem, is suitably replaced by a multimap involving the normal operator to the adjusted sublevel sets. Using this variational formulation, we are able to prove the existence of equilibrium points by using arguments from the set-valued analysis and non-convex analysis.
A blocking set in a plane is a set of points that meets every line. It is called non-trivial if it does not contain a line. A blocking set is minimal if it is minimal subject to set theoretical inclusion. There are classical results on the possible sizes of minimal blocking sets, due to Bruen, Bruen-Thas, Blokhuis, Ball Gacs, Sziklai and the speaker. We will try to survey these result. An almost blocking set is a set of points which "almost" meets all lines, that is there are only few lines that are disjoint from it. We will show some conditions (specify what "few" means) that guarantee that an almost blocking set can be obtained from a blocking by deleting not too many points. Again, there are some old results by Erdos and Lovasz in this directions. We will mention recent such results by Zsuzsa Weiner and the speaker.
In the group theory, ”arithmetical” properties of a group G are the properties which are defined by some arithmetical parameters of G.
Let G be a finite group. The spectrum of G is the set omega(G) of orders of all its elements. The subset pi(G) of prime elements of omega(G) is called prime spectrum of G. The spectrum omega(G) of a group G defines its prime graph (or Grünberg–Kegel graph) Gamma(G) with vertex set pi(G), in which any two different vertices p and q are adjacent if and only if the number pq belongs to the set omega(G). The spectrum, the prime spectrum and the prime graph of a finite group G give examples of arithmetical parameters of G.
Such invariants of a group G as sets of composition and chief factors of G with details of action of G on its chief factors are called the ”normal structure” of G . Cross impact of arithmetical properties of a finite group and its normal structure is well known.
In the present talk we will discuss some questions on the finite prime spectrum minimal, prime graph minimal and spectrum minimal groups. In particular, we will describe all the cases when the prime graphs of a finite simple group and of its proper subgroup coincide and spectrums of a finite simple group and of its proper subgroup coincide.





The Ring of Fire is a problem that baffled me for 25 years. Here it is: You are given a circle of five integers; some positive, some negative, and the sum of all of them is positive. As long as there is at least one negative number in the ring, select one and then 'pop' it by replacing it with its absolute value and then adding the negative version to both of its neighbours. In symbols, replace b -c d with b-c c d-c. Notice that this leaves the sum unaffected. For instance we could have
-1 6 2 -5 1
Popping the -5 gives
-1 6 -3 5 -4
Then popping the -4 gives
-5 6 -3 1 4.
You are to give an elementary proof that this process eventually terminates, i.e., that no matter what sequence of negatives you choose to pop, eventually all of the numbers on the circle will become non-negative. We use rocks and fishes to describe the situation. And we propose a further unsolved problem for which rocks and fishes provide no help.





Racionalna gibanja so zelo uporabno orodje v računalniški grafiki, robotiki in sorodnih področjih. Konstrukcijo navadno razdelimo na dva dela - najprej določimo rotacijski del, nato dodamo translacijski del gibanja. Za interpolacijo danih pozicij se pogosto uporabljajo standardne interpolacijske sheme, ki imajo dve ključni slabosti. Dobljeno gibanje je odvisno od parametrizacije, ki mora biti vnaprej določena, konstruirani polinomi, ki določajo rotacijski del gibanja, pa so relativno visoke stopnje. V doktorski disertaciji bo obravnavan drug pristop - konstrukcija gibanj, ki interpolirajo dano zaporedje pozicij togega telesa (tj. pozicije centra in rotacije) s pomočjo geometrijske interpolacije. Ta pristop ima pomembne prednosti, med drugim to, da je parametrizacija izbrana avtomatično, dobljeno gibanje pa je najmanjše možne stopnje. V doktorski disertaciji bomo predstavili nekatere interpolacijske probleme, izpeljali ustrezne enačbe in razvili interpolacijske sheme za konstrukcije gibanj togih teles z racionalnimi zlepki nizkih stopenj. Vsi teoretični rezultati bodo tudi podkrepljeni z numeričnimi zgledi.
To predavanje je namenjeno predstavitvi teme za doktorsko disertacijo in bo potekalo v slovenskem jeziku.
Let G be a subgroup in the automorphism group of a graph X. The action of G on X is said to be weakly locally projective of type (n(x),q(x)) if for every vertex x of X the stabilizer G(x) of x in G induces on the set of neighbours of x a permutation group, which contains a normal subgroup isomorphic to the special linear group in dimension n(x) over the field of q(x) elements in its natural doubly transitive action on the set of 1-dimensional subspaces of the n(x)-dimensional GF(q(x))-space. Every weakly locally projective action is clearly edge-transitive. If it is also vertex-transitive the word 'weakly' is to be deleted. The main problem is to bound the order of G(x) by a function of n(x) and q(x). It was proved by D. Goldschmidt in his ground breaking paper of 1980 that |G(x)| is at most 384 if n(x)=q(x)=2 for all x; in the vertex-transitive case it amounts to the classical result by W.Tuitte of 1947 that |G(x)| is at most 48. For the locally projective actions the problem was attacked by R.Weiss and others before it was completely solved by V.I.Trofimov at the turn of the century. I would like to discuss locally projective subglaphs in weakly locally projective graphs as a possible path towards reducing the problem from weakly to non-weakly projective actions in the case when q(x)=2 for some vertex x of X.





The Pancake graphis the Cayley graph on the symmetric group of permutations of {1,2,…,n} with the generating set of prefix-reversals. By today two Hamiltonian cycles` constructions are known: the first was given by S. Zaks in 1984 in terms of suffix-reversals,the second was suggested by A. Williams and J. Sawada in 2013 along with the general construction of greedy Prefix-reversal Gray codes.
In this talk we show that both constructions are based on the maximal sets of independent cycles. We define the family of maximal sets of independent cycles of even length in the Pancake graph, present the definition of the Hamiltonian cyclebased on independent cycles in this graph and study the existence of such Hamiltonian cycles. We also show that greedy Prefix-reversal Gray codes are characterized by our construction and provide the necessary condition of existence of these cycles.
At the end we present the open questions for the related research.
This work is joint work with Elena Konstantinova (Sobolev Institute of Mathematics and Novosibirsk State University, Novosibirsk, Russia).
In this talk we present a construction of a rigid body motion with point trajectories being rational spline curves of degree eight joining together with G^3 smoothness, which means that also the torsion is continuous.
The motion is determined through the interpolation of positions and derivative data up to order three in the geometric sense. Nonlinearity involved in a spherical part of construction results in a single univariate quartic equation which yields solutions in a closed form. We give some sufficient conditions on the regions for the curvature data, implying the existence of a real admissible solution. The algorithm how to choose appropriate data is presented too. The theoretical results are substantiated with numerical examples.
These results are joint work with Marjeta Krajnc and Vito Vitrih.




In this talk we present a broader theoretical framework useful in studying the properties of so-called generalized bent functions. We give the sufficient conditions (and in many cases also necessary) for generalized bent functions when these functions are represented as a linear combination of: generalized bent; Boolean bent; and a mixture of generalized bent and Boolean bent functions. These conditions are relatively easy to satisfy and by varying the variables that specify these linear combinations many different classes of generalized bent functions can be derived. In particular, based on these results, we provide some generic construction methods of these functions and demonstrate that some previous methods are just special cases of the results given in this talk.
Consider the graph with the vertex set formed by all $n\times n$ invertible hermitian matrices with coefficients in a finite field $\mathbb{F}_{q^2}$, where two matrices form an edge $\{A,B\}$ if and only if the rank of $A-B$ is one.
In a seminar talk about a year ago I showed that this graph is a core (the case $q=3$ was not considered), which means that all its endomorphisms are automorphisms.
In this talk I will describe the characterization of all endomorphisms (i.e. automorphisms) for $q\geq 4$.





The graph isomorphism problem is a computational problem of deciding whether two given graphs are isomorphic. It’s not known whether the problem can be solved in a polynomial time or it’s an NP- complete. In our lecture we present a well-known Weisfeiller-Leman (WL) algorithm which solves some particular cases of the problem. It will be shown how WL-algorithm yields a special class of colored graphs known as coherent configurations. We’ll show the basic properties of those objects and focus on a special class of them known as association schemes. Association schemes play an important role in algebraic graph theory.
In this PhD thesis we study the isomorphism problem of bi-Cayley graphs and the related question of classifying finite BCI-groups. More precisely, the following questions/problems are considered:
(i) Find effective, sufficient and necessary conditions for the isomorphism of two cyclic bi-Cayley graphs.
(ii) Which groups are 3-BCI-groups?
(iii) Which cubic bi-Cayley graphs are BCI-graphs?
(iv) Which cyclic balanced configurations have the CI-property?
(v) Analytical enumeration of balanced cyclic configurations.
Problem (i) is solved for tetravalent graphs. Problem (ii) is solved for nilpotent groups. We contribute to Problem (iii) by proving that all connected cubic arc-transitive bi-Cayley graphs over abelian groups are BCI-graphs. Regarding Problem (iv), we prove that all cyclic balanced configurations have the CI-property for which the number of points is either a product of two distinct primes, or a prime power. Regarding Problem (v), we derive a close formula for the number of connected cyclic configurations of type (v_3).



The graph isomorphism problem is a computational problem of deciding whether two given graphs are isomorphic. It’s not known whether the problem can be solved in a polynomial time or it’s an NP- complete. In our lecture we present a well-known Weisfeiller-Leman (WL) algorithm which solves some particular cases of the problem. It will be shown how WL-algorithm yields a special class of colored graphs known as coherent configurations. We’ll show the basic properties of those objects and focus on a special class of them known as association schemes. Association schemes play an important role in algebraic graph theory.





The Virtual Element method is a very recent variant of Finite Element Methods, appeared on the scene a couple of years ago. The method could be seen as a combination of Finite Element Methods and Mimetic Finite Differences. In particular it allows, at the same time, the use of very general decompositions of the computational domain (in almost arbitrary polygons or polyhedra), and the use of the (more elegant and more clarifying) Galerkin framework for the analysis and the error estimates. The talk, addressed to a rather general audience of mathematicians, will describe first the general idea of the method on a very simple problem like Poisson problem in 2 dimensions, and then give some very quick hints on various generalizations, including 3D problems, Stokes problem, Kirchhoff plates, variable coefficients, mixed formulations, etc. Much more details could be given, after the lecture, to the interested people. Several papers (both on the basic principles and on further extensions) can be found (and downloaded) on the web page of the speaker: http://www.imati.cnr.it/brezzi/rec_pubbl.html (the newest are at the end).
Lectures will be given by Stephen Wilson throughout the spring semester.
Tentative schedule:
Every Monday, Tuesday and Thursday, starting on Monday, February 16, 2015 and ending on Thursday, June 4, 2015.
Monday:
16:00 - 17:00 FAMNIT-POSTA
Tuesday:
12:00 - 13:00 FAMNIT-MP1
Thursday:
15:00 - 16:00 FAMNIT-MP1
Course overview:
After a brief overview of group actions on sets, we will discuss abstract objects which have relatively large symmetry groups:
Maps:
Rotary, Chiral, Reflexible
Classifications and Families
Automorphism groups of surfaces
Orientable and not
Operators
Polytopes and Maniplexes:
Definitions and relations
Rotary, chiral and reflexible
Orientable and not
Even more operators
Graphs:
Edge-transitivity
Dart-transitive
1/2-arc-transitive
Semisymmetric
Families and sporadic examples
Constructions:
By parameters
From diagrams
from smaller graphs.
Welcome!
Freeman's centralization for a given centrality index is a measure of how central a vertex is regarding to how central all the other vertices are with respect to the given index. The well studied Wiener index (the Wiener number) of a graph G is equal to the sum of distances between all pairs of vertices of G . In the talk I will present the centralization of Wiener index, in particular, we will determine the graphs on n vertices which attain the maximum or minimum value.




Following the terminology of Kammer and Tholey, we say that an orientation of a graph is 1-perfect if the out-neighborhood of every vertex induces a tournament, and that a graph is 1-perfectly orientable (1-p.o. for short) if it has a 1-perfect orientation. The notion of 1-p.o. graphs was introduced by Skrien (under the name B_2-graphs), where the problem of characterizing 1-p.o. graphs was posed. By definition, 1-p.o. graphs are exactly the graphs that admit an orientation that is an out-tournament. (A simple arc reversal argument shows that that 1-p.o. graphs are exactly the graphs that admit an orientation that is an in-tournament. Such orientations were called fraternal orientations in several papers.)
1-p.o. graphs form a common generalization of chordal graphs and circular arc graphs. While they can be recognized in polynomial time via a reduction to 2-SAT, little is known about their structure. We prove several results related to the structure of 1-p.o. graphs. First, we give a characterization of 1-p.o. graphs in terms of edge clique covers, similar to a known characterization of squared graphs due to Mukhopadhyay. We exhibit several examples of 1-p.o. and non-1-p.o. graphs. The examples of non-1-p.o. graphs include two infinite families: the complements of even cycles of length at least 6, and the complements of odd cycles augmented by a component consisting of a single edge. We identify several graph transformations preserving the class of 1-p.o. graphs. In particular, we show that the class of 1-p.o. graphs is closed under taking induced minors. We also study the behavior of 1-p.o. graphs under some operations that in general do not preserve the class, such as pasting along a clique and the join. The result for the join motivates the problem of characterizing the 1-p.o. co-bipartite graphs. We show that all the presented examples of non-1-p.o. graphs are minimal forbidden induced minors for the class of 1-p.o. graphs. As our main results we obtain complete characterizations of 1-p.o. graphs within the classes of complements of forests and of cographs.
Joint work with Martin Milanič.













