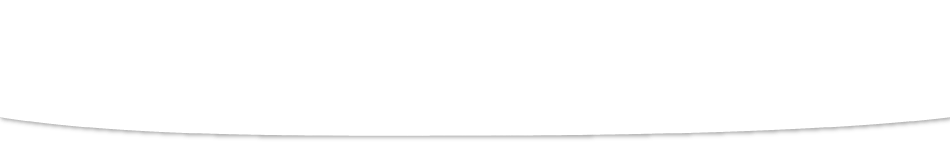Mathematical Research Seminar - Archive

The family of generalized Petersen graphs G(n,k), introduced by Coxeter et al. [Coxeter, H. et al. (1950), ‘Self-dual configurations and regular graphs’, Bull. Amer. Math.Soc 56, 413--455.] and named by Mark Watkins (1969), is a family of cubic graphs formed by connecting the vertices of a regular polygon to the corresponding vertices of a star polygon. The Kronecker cover KC(G) of a simple undirected graph G is a special type of bipartite covering graph of G, isomorphic to the direct (tensor) product of G and K2. We characterize all the members of generalized Petersen graphs that are Kronecker covers, and describe the structure of their respective quotients. We observe that some of such quotients are again generalized Petersen graphs, and describe all such pairs.

The Weiss Conjecture has stimulated much study of symmetric graphs, especially concerning the order of vertex-stabilisers. The conjecture roughly asserts that in a locally-primitive symmetric graph, the vertex-stabiliser is not too large compared to the valency. The conjecture implies that “local properties” have a global impact, since this also bounds the order of the automorphism group. Further refinements to this conjecture were suggested, first by Praeger who asked if local quasiprimitivity might be sufficient, and then by Potocnik-Spiga-Verret who found semiprimitive groups are the key. This latter class of permutation groups has not been well studied, and indeed only recently - 2008 - appeared in the literature. In seeking to understand the validity of these conjectures, I have been motivated to study semiprimitive groups in a more general context, and try to make our understanding of this class of groups equal to that of the well studied class of primitive groups. In this talk I’ll mention some progress towards that, and highlight the impact the results have already had on the aforementioned conjectures.

A nut graph is a singular graph of nullity one with a kernel eigenvector having no component equal to 0. We attack the following problem. For each valence d, determine all values of n such that a regular, d-valent nut graph of order n exists. We solve this problem completely for d \leq 4. The main tool in our approach is the Fowler extension of a graph. If time permits we will also give a demonstration of a short sagemath program that tests whether a given graph is a nut graph. This talk is based on the work in progress with John Baptist Gauci and Irene Sciriha. In the proof of case d=4 the help of Patrick Fowler and Nino Bašić is acknowledged.

Let G be a graph with n vertices, S=\mathbb{K}[x_1,\dots,x_n] be the polynomial ring in n variables over a field \mathbb{K} and I(G) denote the edge ideal of G.

We survey a number of recent studies of the Castelnuovo-Mumford regularity of the edge ideal of G. Our focus is on bounds and exact values for the regularity in terms of combinatorial data from associated graphs.

In addition, for every collection \mathcal{H} of connected graphs with K_2\in \mathcal{H}, we introduce the notions of ind-match_{\mathcal{H}}(G) and min-match_{\mathcal{H}}(G). We will improve the inequalities for regularity of S/I(G).

Let G be a group and S\subseteq G. A Haar graph of G with connection set S has vertex set \Z_2\times G and edge set \{(0,g)(1,gs):g\in G{\rm\ and\ }s\in S\}. Haar graphs are then natural bipartite analogues of Cayley digraphs. We first examine the relationship between the automorphism group of a Cayley digraph of G with connection set S and a Haar graph of G with connection set S. We establish that the automorphism group of a Haar graph contains a natural subgroup isomorphic to the automorphism group of the corresponding Cayley digraph. In the case where G is abelian, we then give four situations in which the automorphism group of the Haar graph can be larger than the natural subgroup corresponding to the automorphism group of the Cayley digraph together with a specific involution, and analyze the full automorphism group in each of these cases. As an application, we show that all s-transitive Cayley graphs of generalized dihedral groups have a quasiprimitive automorphism group, can be ``reduced" to s-arc-transitive graphs of smaller order, or are Haar graphs of abelian groups whose automorphism groups have a particular permutation group theoretic property.

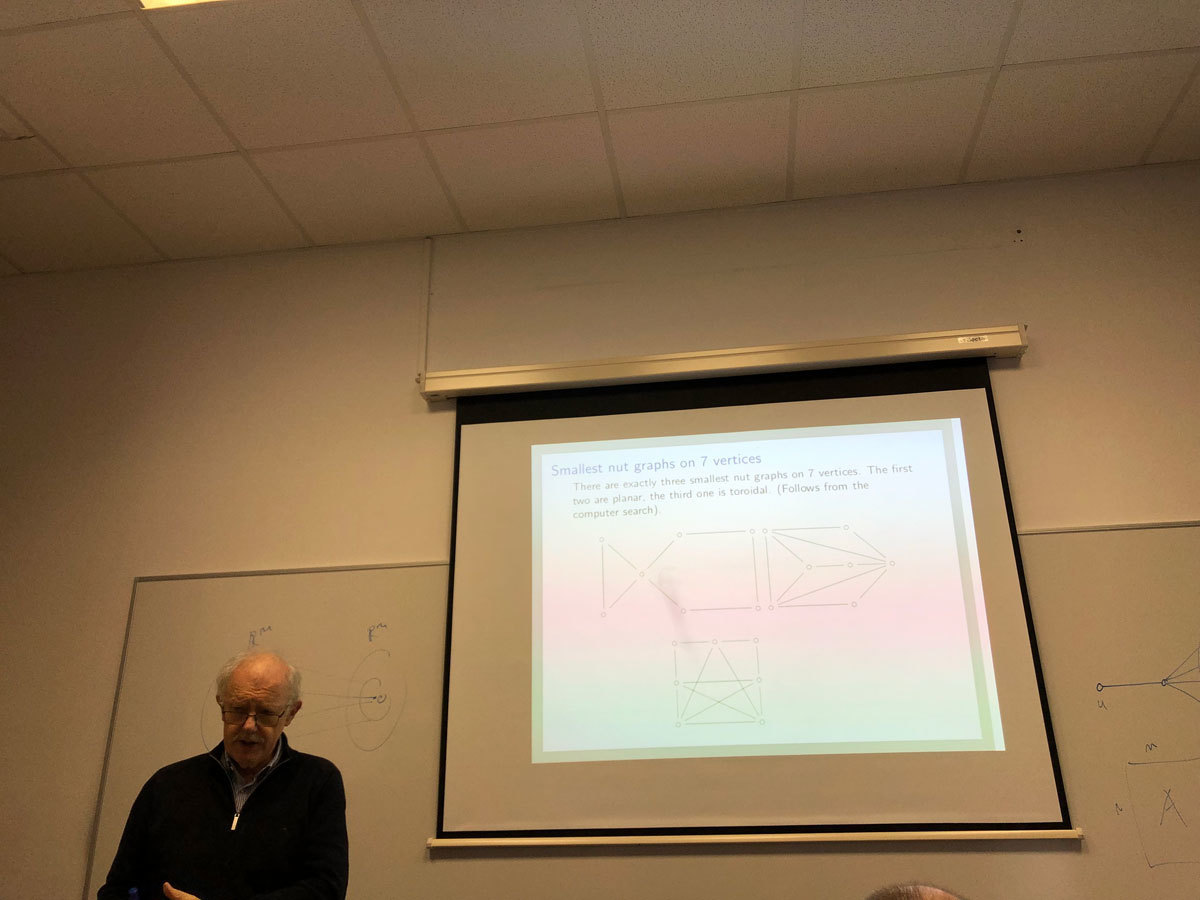
Roughly speaking, the celebrated central limit theorem says that a sum of many small independent random variables with sufficiently nice distributions approximately follows the normal (Gaussian) distribution. An important issue is the estimation of the error in the normal approximation. Numerous approaches have been suggested. In 1962, Slepian suggested elegant gradual replacement of the original sum with a Gaussian random variable. This approach is essentially equivalent to Stein's method introduced in 1970, which arises from a different idea.

Though relatively old, Stein's method is still a highly active field of research. This is highly due to its flexibility. In particular, Stein's method does not only work for sums of independent random variables, but also for families with various kind of dependence structure. We shall focus on the so called local dependence.

We discuss a new family of cubic graphs, which we call $SGP$-graphs, that bears a close resemblance to the family of generalized Petersen graphs; both in definition and properties. The focus of our paper is on determining the algebraic properties of graphs from our new family. We look for highly symmetric graphs, e.g., graphs with large automorphism groups, vertex- or arc-transitive graphs. In particular, we present arithmetic conditions for the defining parameters that guarantee that graphs with these parameters are vertex-transitive or Cayley, and we find one arc-transitive $SGP$-graph which is neither a $CQ$ graph of Feng and Wang, nor a generalized Petersen graph. 

Joint work with Katarina Jasencakova and Robert Jajcay.

For a given graph search algorithm and a graph G, a vertex v is said to be an end-vertex if there exists a corresponding search ordering of the vertices such that v is the last vertex in this ordering. It is known that the complexity of recognizing the end-vertices in general graphs is NP-hard for several search algorithms, such as Breadth First Search, Depth First Search, and their lexicographic variants. This motivated the study of end-vertices with respect to some other search algorithms. In this work we consider Maximum Cardinality Search (MCS) and Maximum Neighborhood Search (MNS) and present results concerning the complexity of the end-vertex problem with respect to these search methods. We give some proofs of NP-completeness of this problem in general graphs, as well as polynomial-time algorithms, when a graph is restricted to belong to certain graph classes. Joint work with J. Beisegel, C. Denkert, E. Köhler, M. Krnc, R. Scheffler, and M. Strehler.

We consider a bi-level knapsack problem, where two players, the leader and the follower, are each associated with a subset of the items. The leader may offer profits for its items to the follower, before the follower selects a subset of all items in order to utilize a bounded resource in the best possible way, i.e. trying to maximize the overall profit.

The leader receives as pay-off only the profits from those items of its associated subset that were included in the overall solution chosen by the follower. This pay-off is then reduced by the profits offered to the follower. The resulting setting is a Stackelberg strategic game. The leader has to resolve the trade-off between offering high profits as incentives to the follower and offering low profits to gain high pay-offs.

We analyse the problem for the case where the follower solves the resulting knapsack problem to optimality, and obtain a number of strong complexity results. Then we invoke a typical assumption of the literature that the follower's computation power is bounded. Under this condition, we study three natural Greedy-type heuristics applied by the follower. The solution structures and complexities of the resulting problems are investigated and solution strategies are derived, in particular an ILP model, but also (pseudo)polynomial algorithms, when possible.

Joint work with Gaia Nicosia, Andrea Pacifici and Joachim Schauer

Matrices whose commutant is either maximal or minimal with respect to set-inclusion were classified in 2005 by Dolinar and Šemrl in their pursuit towards classification of bijections which preserve zeros of Lie product. The classification which they obtained  is valid only for complex matrices. Recently, we extended their classification in several directions:
(a) For matrices over an arbitrary field. Besides the  classes that were obtained in the complex case some new possibilities are possible here.
(b) We also investigated problems of these kinds within certain subclasses of (complex) matrices, in particular within doubly stochastic matrices.
(c) Instead of commutativity one may further consider the commutativity up to a factor \xi, defined by AB = \xi BA and classify matrices which are extremal with respect to this relation.

The aim of the talk is to present the obtained results. This is joint work with many collaborators.

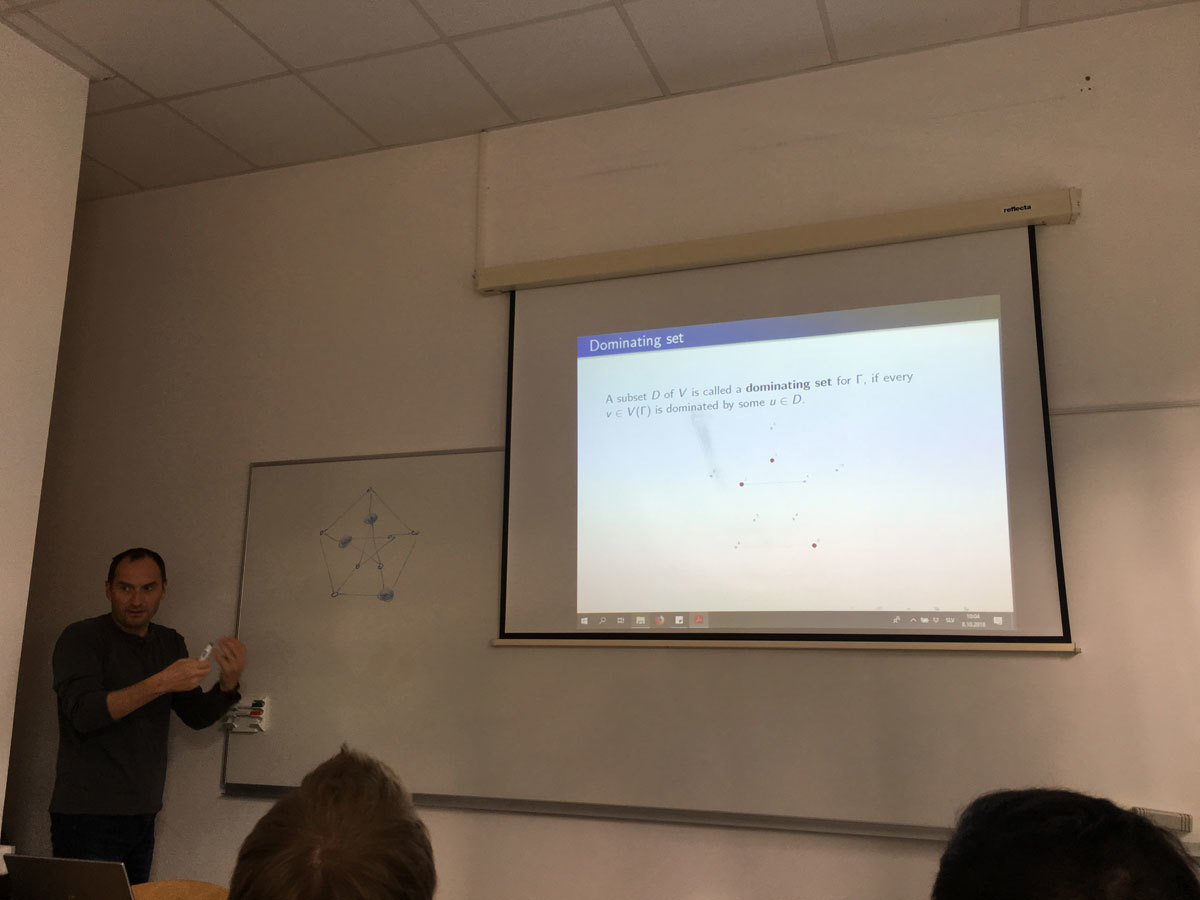
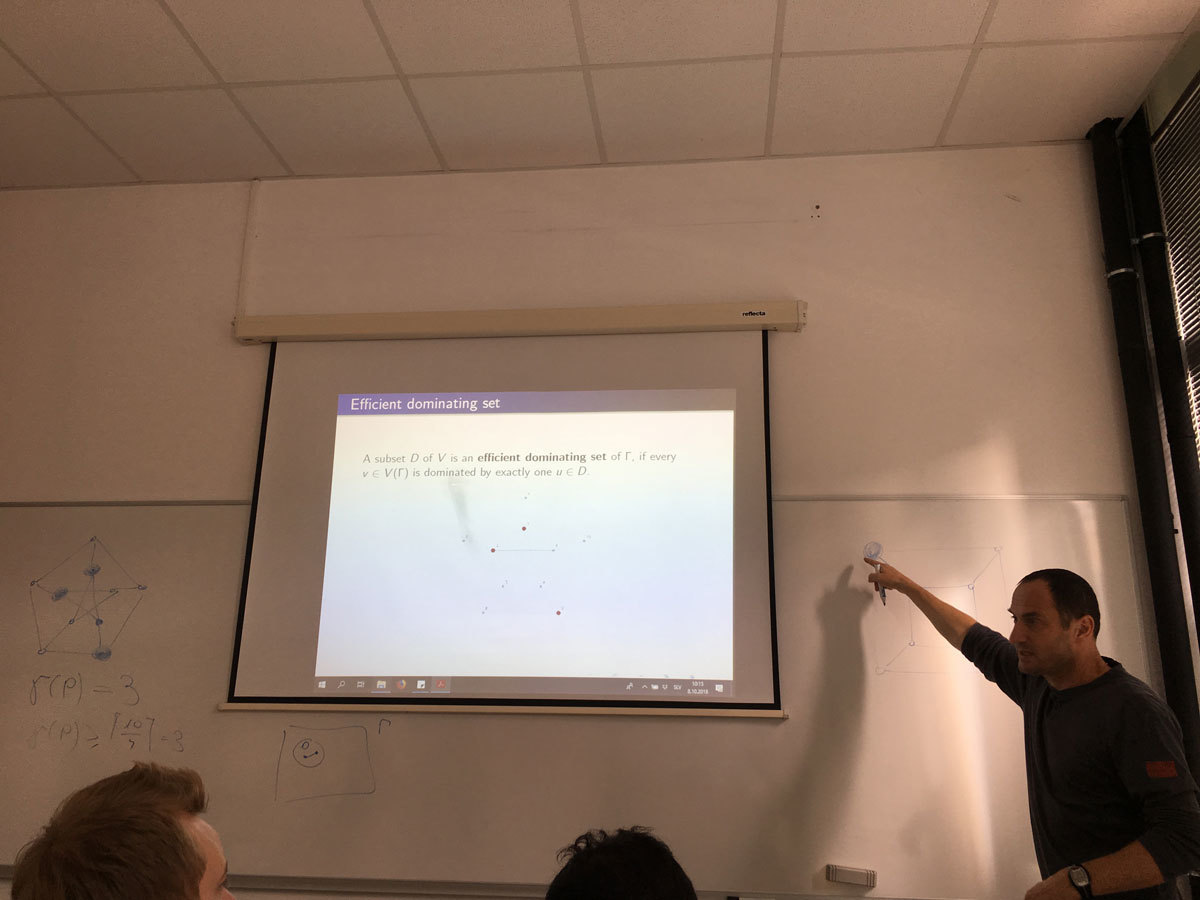
An independent set D of vertices in a graph is an efficient dominating set when each vertex not in D is adjacent to exactly one vertex in D. In this talk we give a classification of cubic and quartic Cayley graphs on abelian groups, which admit efficient dominating set.

Joint work with Sibel Ozkan and Cafer Celiskan.

Determining the genus of graphs is one of the fundamental NP-complete problems. Thus it makes sense to ask whether the genus can be efficiently approximated. By using the Szemeredi Regularity Lemma, and by analysing the genus of random and quasirandom graphs, we are able to find a PTAS (polynomial-time approximation scheme) to approximate the genus of dense graphs within arbitrarily small error.

This is joint work with Yifan Jing.

The First Koper - Bahia Blanca Workshop on Structural and Algorithmic Graph Theory
UP FAMNIT, Glagoljaska 8, Koper, Velika predavalnica
Wednesday, July 4, 2018, 9:30-12:00

9:30-10:00 Nevena Mitrovic (University of Primorska), On the End-Vertex Problem
10:00-10:30 Martin Safe (Universidad Nacional del Sur, Bahia Blanca, Argentina), Convex p-partitions of bipartite graphs
10:30-11:00 break 
11:00-11:30 Martin Milanic (University of Primorska), 1-Sperner hypergraphs and new characterizations of threshold graphs
11:30-12:00 Nina Chiarelli (University of Primorska), Improved algorithms for k-domination and total k-domination in proper interval graphs

======================================================
ABSTRACTS OF TALKS
======================================================

Nevena Mitrovic, On the End-Vertex Problem

For a given graph search algorithm and a graph G, a vertex v is said to be an end-vertex if there exists a corresponding search ordering of the vertices such that v is the last vertex in this ordering. It is known that the complexity of recognizing the end-vertices in general graphs is NP-hard for several search algorithms, such as Breadth First search, Depth First Search, and their lexicographic variants. This motivated the study of end-vertices with respect to some other search algorithms. In this work we consider the Maximum Cardinality Search (MCS) and the Maximum Neighborhood Search (MNS) and present the results concerning complexity of the end-vertex problem with respect to these search methods.

The talk is based on joint work with Jesse Beisegel, Carolin Denkert, Ekkehard Koehler, Matjaz Krnc, Robert Scheffler, and Martin Strehler.
(An extended abstract of this work will be published in the proceedings of ICGT 2018.)

======================================================

Martin Safe, Convex p-partitions of bipartite graphs

A set X of vertices in a graph is convex if no shortest path between two vertices in X contains a vertex outside of X. A convex p-partition of a graph is a partition of its vertex set into p nonempty convex sets. It is known that, for each integer p greater than or equal to 2, deciding whether any given graph has a convex p-partition is an NP-complete problem. We show that, for each fixed positive integer p, all convex p-partition of any given bipartite graph G can be enumerated in polynomial time.

This is joint work with Luciano Grippo, Martin Matamala, and Maya Stein.

Reference:
Grippo, Luciano N., Martin Matamala, Martin D. Safe, and Maya J. Stein. Convex p-partitions of bipartite graphs. Theoretical Computer Science 609 (2016): 511-514.
https://doi.org/10.1016/j.tcs.2015.11.014

======================================================

Martin Milanic, 1-Sperner hypergraphs and new characterizations of threshold graphs

A hypergraph is Sperner if no hyperedge contains another one. A Sperner hypergraph is equilizable (resp., threshold) if the characteristic vectors of its hyperedges are the (minimal) binary solutions to a linear equation (resp., inequality) with positive coefficients. These combinatorial notions have many applications and are motivated by the theory of Boolean functions and integer programming. We introduce the class of 1-Sperner hypergraphs, defined by the property that for every two hyperedges the smallest of their two set differences is of size one. We characterize this class of Sperner hypergraphs by a decomposition theorem and derive several consequences from it. Furthermore, we present several applications of 1-Sperner hypergraphs and their structure to graphs. In particular, we consider the classical characterizations of threshold and domishold graphs and use them to obtain further characterizations of these classes in terms of 1-Spernerness, thresholdness, and 2-asummability of their vertex cover, clique, dominating set, and closed neighborhood hypergraphs. 

The talk is based on joint work with Endre Boros and Vladimir Gurvich.

Link to preprints: 
https://arxiv.org/abs/1510.02438
https://arxiv.org/abs/1805.03405

======================================================

Nina Chiarelli, Improved algorithms for k-domination and total k-domination in proper interval graphs
 
Given a positive integer k, a k-dominating set in a graph G is a set of vertices such that every vertex not in the set has at least k neighbors in the set. A total k-dominating set, also known as a k-tuple total dominating set, is a set of vertices such that every vertex of the graph has at least k neighbors in the set. The problems of finding the minimum size of a k-dominating, resp. total k-dominating set, in a given graph, are referred to as k-domination, resp. total k-domination. These generalizations of the classical domination and total domination problems are known to be NP-hard in the class of chordal graphs, and, more specifically, even in the classes of split graphs (both problems) and undirected path graphs (in the case of total k-domination). On the other hand, it follows from recent work by Kang et al. (2017) that these two families of problems are solvable in time O(|V(G)|^{6k+4}) in the class of interval graphs. In this work, we develop faster algorithms for k-domination and total k-domination in the class of proper interval graphs. The algorithms run in time O(|V(G)|^{3k}) for each fixed k >= 1 and are also applicable to the weighted case. 

The talk is based on joint work with Tatiana Romina Hartinger, Valeria Alejandra Leoni, Maria Ines Lopez Pujato, and Martin Milanic.

Link to preprint: https://arxiv.org/abs/1803.04327
(An extended abstract will be published in the proceedings of ISCO 2018.)

Quantum Computers are built on the principles of Quantum Mechanics. It has been proved that many difficult problems can be solved by quantum computers. We intend to introduce quantum computing and discuss some quantum algorithms. We also intend to explore the connections between Boolean functions and quantum computing. 

The topics to be discussed are as follows: 

- Introduction to Quantum Mechanics and Quantum Information.  Quantum States, Operators and Measurements. 
- BB84: A quantum key exchange protocol. 
- Quantum Entanglement. Quantum Teleportation. 
- Quantum Circuits: Single qubit gates, multiple qubit gates, design of quantum circuits. 
- Quantum Algorithms:  Deutsch's algorithm, Deutsch's-Jozsa algorithm. 
- Grover search and Its Geometric interpretation.  
- Implementing quantum algorithms on IBM's quantum computer IBM-Q. 
- Boolean functions and quantum computing.

In this talk I want to present the connection between the so-called cluster expansion and relation between species of graphs.
Cluster expansion is a way of dismantling highly complex correlation patterns in probability distributions describing the long term behaviour of high dimensional dynamical systems. The terms of these expansions are labeled by species of graphs, like multi-rooted simple or double connected graphs. Changing the expansion parameter is related to functional relations between the generating functions of different species.
Finally, I will discuss how one can prove convergence of theses expansion, which requires to estimate them by an expansion labeled by trees.

A {\em pseudo-Boolean function}  is a real-valued function f(x)=f(x_1,x_2,\ldots,x_n) of n binary variables. It is well-known  that every pseudo-Boolean function can be uniquely represented as a multilinear polynomial in its variables.

\emph{Nonlinear binary optimization problems}, or \emph{pseudo-Boolean optimization} (PBO) \emph{problems}, of the form 
\min \{ f(x) : x \in \{0,1\}^n \},
where f(x) is a pseudo-Boolean polynomial,  have attracted the attention of numerous researchers for more than 50 years.  These problems are notoriously difficult, as they naturally encompass a broad variety of models such as maximum satisfiability, max cut, graph coloring, image restoration, and so on.

In this talk, I present recent results (obtained in collaboration with Martin Anthony, Endre Boros, Aritanan Gruber, and Elisabeth Rodriguez-Heck) regarding the size of reformulations of nonlinear PBO problems as quadratic PBO problems.

SLIDES

The talk gives a light introduction to the theory of combinatorial (impartial) games and the Sprague-Grundy theory. Then we consider a generalization of the well-known game of NIM, and show several results about such generalizations.

Joint work with Vladimir Gurvich, Nhan Bao Ho, Kazuhisa Makino, and Peter Mursic.

Nowadays nobody doubts the significance of the applications of graph theory to other sciences or to real world problems. This workshop emphasizes the diversity of these applications.

However, not everyone outside of graph theory realizes that the powerful combinatorial methods found in graph theory have also been used to prove significant and well-known results in a variety of areas of pure mathematics. That is, that there are applications of graph theory to other areas of pure mathematics as well. Perhaps the best known of these methods are related to matching theory. For example, results from this area can be used to prove Dilworth's chain decomposition theorem for finite partially ordered sets. A well-known application of matching in group theory shows that there is a common set of left and right coset representatives of a subgroup in a finite group. Also, the existence of matchings in certain infinite bipartite graphs played an important role in Laczkovich's affirmative answer to Tarski's 1925 problem of whether a circle is piecewise congruent to a square [1]. Other applications of graph theory to pure mathematics may be found scattered throughout the literature, e.g. see [2]. There, among other examples, matching theory is applied to give a very simple constructive proof of the existence of Haar measure on compact topological groups.

In this talk we will present an examples of such applications of graph theory to number theory, measure theory, and analysis, respectively. On purpose two of these applications are applications of graph theory (finite mathematics) to continuous mathematics, which we find more impressive. Further criteria for choosing these examples were that the theorem is fundamental, widely known, and the graph theory proof of the theorem is the most elegant and/or the shortest one. In other words, the proof should exhibit the strength and elegance of graph-theoretic methods.

References
[1] M. Laczkovich, M. Equidecomposability and discrepancy; a solution of Tarski's circle-squaring problem. J. Reine Angew. Math. 404 (1990), 77--117.
[2] L. Lóvasz, L. Pyber, D. J. A.Welsh, and G. M. Ziegler, Combinatircs in pure mathematics, in Handbook of Combinatorics (R.L. Graham, M. Grotschel, and L. Lovasz, eds.), Elsevier, 1996.

For a positive integer k, we say a simple graph G is a k-circulant if it admits a semiregular automorphism that partitions its vertex-set into k orbits of the same size. The study of k-circulant graphs is extensive, specially that of vertex- and arc-transitive ones, and some families of k-circulants, for small values of k, are of particular interest. We provide a complete classification, along with some structural results, for cubic vertex-transitive 3-circulants.

Kaplan, Lev and  Roditty [1] introduced a notion of zero-sum partitions of subsets in Abelian groups. Let \Gamma be an Abelian group of order n. We shall say that \Gamma has the zero-sum-partition property (ZSP-property) if every partition n-1 = r_1 + r_2 + \ldots + r_t of n-1, with r_i \geq 2 for 1 \leq i \leq t and for any possible positive integer t, there is a partition of \Gamma - \{0\} into pairwise disjoint subsets A_1, A_2,\ldots , A_t, such that |A_i| = r_i and \sum_{a\in A_i}a = 0 for 1 \leq i \leq t.  They conjectured that every Abelian group \Gamma, which is of odd order or contains exactly three involutions, has the ZSP-property. The conjecture was recently proved by Zeng [2].

In this talk we show some applications of the ZSP-property of groups in some graph labeling problems.

[1] G. Kaplan, A. Lev, Y. Roditty, On zero-sum partitions and anti-magic trees, Discrete Math. 309(8) (2009), 2010--2014.
[2] X. Zeng, On zero-sum partitions of abelian groups. Integers 15 (2015), Paper No. A44, 16 pp.

A variant of Vehicle Scheduling Problem (VSP) arising from the sugar beet transportation in a sugar factory in Serbia is introduced. The objective of the considered VSP is to minimize the required transportation time under problem-specific constraints. The considered VSP is first modelled as Mixed Integer Quadratically Constrained Program (MIQCP) and then reformulated to the equivalentMixed Integer Linear Program (MILP). In addition, it is proved that the considered VSP is NP-hard. Both MIQCP and MILP formulations were used within the framework of Lingo 17 solver on the set of real-life and generated problem instances. The proposed formulations enable Lingo 17 solver to produce optimal or feasible solutions for smaller-size problem dimensions. On these test examples, MILP reformulation showed to be superior over the MIQCP model in terms of solution quality and running times required by Lingo 17 solver.

This is a joint work with Anokić Ana, Tatjana Davidović and Đorđe Stakić.

In this talk I will give a brief survey of my research in the field of cryptography conducted for the past twenty years. The importance of developing discrete mathematical structure suitable for real-life applications in symmetric-key encryption schemes (and cryptography in general) will be motivated on a non-professional level (students will not be bored), thus rather providing a big picture than insisting on unnecessary details related to my scientific work. Some highlights of my research work will be mentioned related to both applicative aspects of discrete mathematical structures, such as the use of Boolean functions to design orthogonal sequences for CDMA applications, and also to purely mathematical context such as the construction of semi-fields and projective/affine spaces. This will lead us to some nice problems (open for more than 20 years) that concern the theory of finite fields or Boolean functions which can be formulated in a compact and elegant way. These problems are exactly the kind of problems that arise our intrigue and give us a motivation to keep on with research. The issue of academic freedom to deal with these »hard« problems will be also briefly addressed.

Partial cubes are isometric subgraphs of hypercubes. Median graph is a graph in which every three vertices u,v and w have a unique median: a vertex m that belongs to shortest paths between each pair of u,v and w. Median graphs present one of the most studied subclasses of partial cubes. We determine the Smith normal form of the distance matrices of partial cubes and the factorisation of Varchenko determinant of product distance matrices of median graphs.

The deep relationship between the Laplacian, heat equation and Brownian motion has been explored with much success over the past decades. Recently much attention has been attracted by fractional Laplacians, non-local equations and jump processes allowing to capture new phenomena and offer a new prespective on the classical theory. I will highlight some aspects of a probabilistic understanding of solutions of non-local equations involving some specific models.

Mathematics is all around us. It’s behind all the algorithms that make computers work so anything that involves computing and technology needs maths. If you can do maths you are essentially able to invent the future.

When I was a student I was told “there are no jobs for a maths graduate”. Clearly wrong. I’ll tell you a bit of my journey into maths, the kinds of maths I love and use - the mathematics of symmetry - my links with mathematics in Slovenia - how this is a link between mathematics and life - how there is a place in maths for both women and men.

In this talk we present the main topics, research questions and the expected results of the proposed PhD thesis.

In the PhD Thesis we will focus on open questions and problems which concern the Cage problem and the Degree/Diameter problem for undirected and directed graphs.

Cage Problem (Degree/Girth Problem): Given natural numbers k and g, find the smallest possible number of vertices n(k,g) in a graph of degree k and girth g.

Degree/Diameter Problem: Given natural numbers k and d, find the largest possible number of vertices n(k,d) in a graph of maximum degree k and diameter d.

(Directed) Degree/Diameter Problem: Given natural numbers d and k, find the largest possible number of vertices n_{d,k} in a digraph of maximum out-degree d and diameter k.

In the first part of the PhD thesis we will focus on the bipartite graphs of excess 4, antipodal cages of even girth and small excess and on the excess of the vertex-transitive graphs. We plan to prove the non-existence of infinitely many bipartite (k,g)-graphs of excess 4, the non-existence of almost all potential antipodal cages of even girth and small excess and to improve the Biggs's result which address the existence of the vertex-transitive graphs of given degree and girth.

In the second part we will focus on the Bermond and Bollob\' as question: ``Given a positive integer c>0, does there exist a pair k and d, such that n(k,d)\leq M(k,d)-c?,'' where M(k,d) is the Moore bound. We plan to answer this question combining spectral and real analysis.

In the last part of the PhD thesis we will focus on two problems which concern the degree/diameter problem for directed graphs. We plan to answer the question about the monotonicity of the function n_{d,k} in k and d, and to prove the non-existence of infinitely many (d,k,\delta)-digraphs containing only self repeat vertices.

This thesis would like to extend some concepts of an existing representation theory for closed PL manifolds, called Crystallization Theory. This theory has the peculiarity of using a particular class of regular edge-coloured (multi)graphs (called crystallizations) to represent PL manifolds, so that topological properties can be translated into combinatorial ones (PL invariants of manifolds can be computed directly on the representing graphs).

Firstly, we introduce concepts on Combinatorial Topology and on Graph Theory in order to construct such particular graphs. Then, properties, classic results and the computation of an important topological invariant (Fundamental Group) will be mentioned.

In the main part of the work we study a local operation on a graph, called switching of a \rho-pair, which allows to minimize a graph without changing the underlying PL structure and generalize its property to graphs representing general polyhedra (a sketch of the proof is given).

Then, we focus on the 3-dimensional case. After some basic definitions, we prove that the relations between Heegaard splittings or diagrams and edge-coloured graphs still hold for manifolds with non-empty boundary and that the classical topological invariant, the Heegaard genus, and the totally combinatorial invariant, the regular genus, coincide for all compact 3-manifolds (again a sketch of the proof is described).

Finally, we study the connections between planarity of graphs and regular planar embeddings of edge-coloured graphs: we establish a little result concerning non-planarity of simple graphs that allows to exclude planar simple graphs as representatives of PL n-manifolds, with n\ge 3.

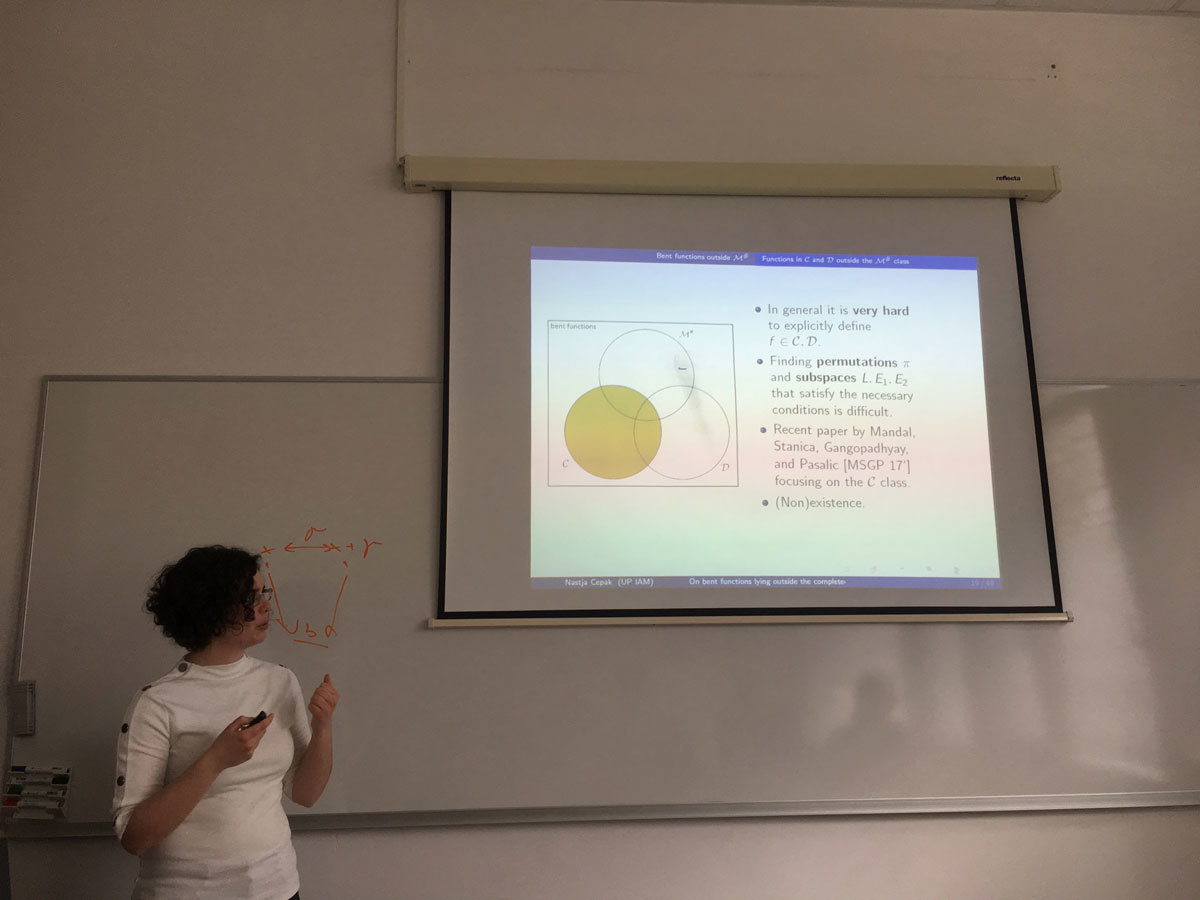
One of the most well known classes of bent functions is the Maiorana-McFarland class M. Knowing in which ways it overlaps with other classes of bent functions and determining whether new constructions yield bent functions that lie outside or inside of it are important questions. We will take a look at a special version of the Rothaus'construction and see if it can generate bent functions lying outside the completed Maiorana-McFarland class M#. Sufficient conditions will be presented for functions within C (and D) class to lie outside the M# class and we will demonstrate examples of such functions in C and show two infinite classes of functions in D outside the M# class. Next, translators will be considered - first linear translators and then their generalisation, the Frobenius translator. Constructions of permutations and bent functions relying on translators will be demonstrated. Finally, constructions of vectorial plateaued functions, permutations and complete permutations using the Maiorana-McFarland class.

In this talk the properties of cubic symmetric graphs will be described. 
Special emphases will be given to a recent characterization of these graphs via the so-called rigid cells.

The course is an introduction to the Polya’s theory in order to answer
questions such as:
-Up to isomorphism, how many graphs on n vertices are there?
-Up to rotational symmetry, how many ways can we color the faces of a cube?
-How many necklaces can be formed using 8 beads of 3 different colors?
The mini-course will be self-contained, and will start by reviewing definitions and main results involving group actions and permutation groups. Important results from permutation groups such as orbit-stabilizer theorem, Burnside's theorem and Polya's enumeration theorem will be proved. These theorems will be followed by many examples and interesting applications.

The updated schedule is as follows:

Wednesday, 28.02.2018: 16:00 - 18:30 - Lecture room: Muzejski 1
Thursday, 01.03.2018:  10:00 - 11:30 - Lecture room: FAMNIT - POŠTA
Friday, 02.03.2018:    10:00 - 12:30 - Lecture room: Muzejski 1

Wednesday, 7.3.2018:   16:00 - 18:30 - Lecture room: Muzejski 4
Thursday, 8.3.2018:    9:30  - 11:00 - Lecture room: FAMNIT-VP
Friday, 9.3.2018:      10:00 - 12:30 - Lecture room: Muzejski 1

(Joint work with Roman Nedela)

Bi-Cayley graphs are graphs admitting a semiregular group of automorphisms with two orbits. A notable cubic subclass of bi-Cayley graphs is the so-called generalized Petersen graphs. Castagna and Prins proved in 1972 that all generalized Petersen graphs except for the Petersen graph itself can be properly 3-edge-colored. In this talk, we are going to discuss the extension of this result to all connected cubic bi-Cayley graphs over solvable groups. Our theorem is a bi-Cayley analogue of similar results obtained by Nedela and Škoviera for Cayley graphs any by Potočnik for vertex-transitive graphs.

An automorphism of a graph is said to be even/odd if it acts on the vertex set of the graph as an even/odd permutation. In this talk, I will present the formula for the number of non-isomorphic graphs of order n admitting an odd automorphism, together with some asymptotic estimates. We will then focus on the existence of odd automorphisms in the class of vertex-transitive graphs. A positive integer n is a Cayley number if every vertex-transitive graph of order n is a Cayley graph. By analogy, a positive integer n is said to be a vertex-transitive-odd number (in short, a VTO-number) if every vertex-transitive graph of order n admits an odd automorphism. We will prove that Cayley numbers congruent to 2 modulo 4, cube-free nilpotent Cayley numbers congruent to 3 modulo 4, and numbers of the form 2p, for p a prime, are VTO numbers. At the other extreme, it is possible that the complete graph K_n is the only connected vertex-transitive graph of order n>2 admitting an odd automorphism. We will prove that this happens if and only if n is a Fermat prime. 

This is joint work with Klavdija Kutnar and Dragan Marušič.

The aim of this talk is to consider the quasiconvex and pseudoconvex functions. One of the reasons for the study of generalized convexity is that convexity usually is a rather rigid assumption, and often it is not satisfied in real-world applications. Instead, the generalized convex functions mantain good properties and it are used in several areas of science, including scalar and vector optimization, operations research, mathematical economics. 

After introducing this class of functions, we will deal with  the role of the generalized convexity in Optimization and in the economic applications.

Lectures will be held:
Wednesday 31st of January 2018. from 10:00 -- 11:00 (FAMNIT-POŠTA)
Friday 2nd of February 2018. from 10:00 -- 12:00 (FAMNIT-POŠTA)

 In my lectures I'll talk about coherent configurations, association schemes and their connection to combinatorics and finite geometry. We also learn how coherent configurations are related to the Graph Isomorphism Problem. Also a brief introduction to the Weisfeiler-Leman algorithm will be given.

Lectures will be:
Wednesday 24th of January 2018. from 11:00 -- 12:30 (FAMNIT-Muzejski1)
Friday 26th of January 2018. from 11:00 -- 12:30 (FAMNIT-Muzejski1)
Monday 29th of January 2018 from 11:00 -- 12:30 (FAMNIT-Pošta)

In this talk we present the main topics, research questions and the expected results of the proposed PhD thesis.

The central theme of the PhD thesis are graphs admitting a considerable degree of symmetry. More precisely, we focus on graphs admitting a vertex- and edge-transitive group of automorphisms. 

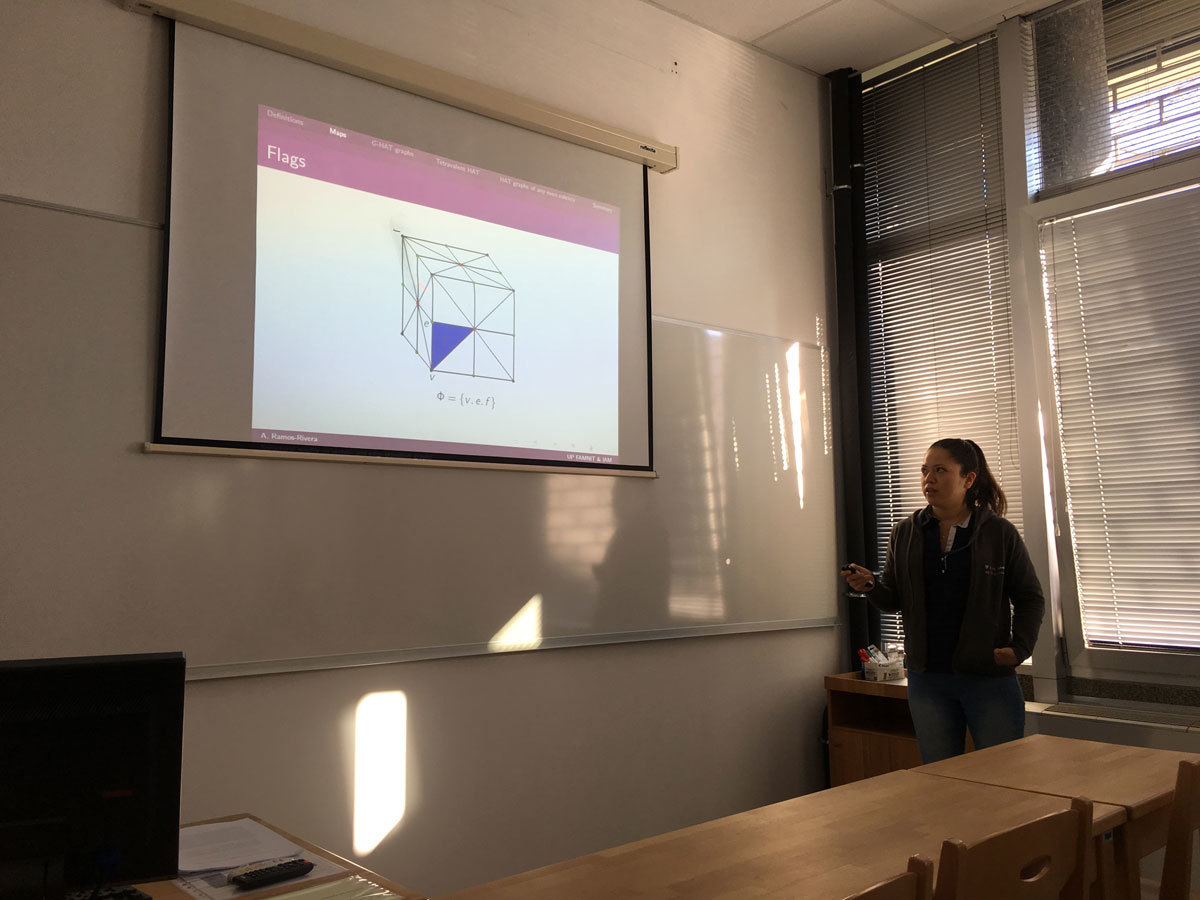
A graph Γ is said to be G-vertex-transitive, G-edge-transitive and G-arc-transitive whenever the subgroup G ≤ Aut(Γ) acts transitively on V(Γ), E(Γ) and A(Γ), respectively. We say that Γ is G-half-arc-transitive (abbreviated by G-HAT) if it is G-vertex- and G-edge-transitive but not G-arc-transitive. In the case of G=Aut(Γ), we omit the prefix G and simply write vertex-transitive, edge-transitive, arc-transitive and half-arc-transitive (abbreviated by HAT).

Let Γ be a G-vertex- and G-edge-transitive graph for some G ≤ Aut(Γ). Then two essentially different possibilities can occur:
(i) Γ is G-arc-transitive.
(ii) Γ is G-half-arc-transitive.

In the first main topic of the PhD thesis we will focus on the situations from the above possibility (i). In particular, we will be interested in the application of the properties of arc-transitive graphs as a tool in the investigation of symmetries of maps. 

In the second and third part of the PhD thesis, we will focus on the situations from the above possibility (ii). We plan to introduce a new parameter of tetravalent G-HAT graphs, giving a better understanding of the structural properties of such graphs. We will study the properties of the graphs with respect to this parameter and use it to relate two important approaches for a possible classification of all tetravalent G-HAT graphs. We will also improve the results on the question of whether the attachment number divides the radius for all tetravalent HAT graphs. 

Finally, we will focus on HAT graphs with valencies greater than four. We will generalize the Bouwer graphs to obtain a much larger family of vertex- and edge-transitive graphs, most of whose members are in fact tightly attached HAT graphs. 

The essence of commutativity relation on a given Magma is captured in its commuting graph which, by definition, is a simple graph on noncentral elements as vertices and where two distinct vertices a,b form an edge if ab=ba. The commuting graph can be an important tool in investigation of nonabelian Magmas which lack the notion of a commutator (say, in semigroups) but can also be studied in nonabelian groups or algebras.

In the talk we aim to show a few examples of isometry transfer problems, i.e., that in certain class of (semi)groups and matrix algebras the commuting graphs are isomorphic if and only if the corresponding algebraic sets are isomorphic. We will also consider realizability questions, i.e., which graph can be obtained as a commuting graph of a semigroup or of a group.

Time permitting, we will further address property recognition for matrix algebras, i.e., how to determine from commuting graph if a matrix has, say, rank-one or is diagonalizable, and/or review basic ideas in classification of homomorphisms of certain commuting (and anti-commuting) graphs.

Mader (1972) proved that every graph of average degree at least 4k contains a (k+1)-connected subgraph, and Alon, Kleitman, Saks, Seymour, and Thomassen (1987) proved that every graph of chromatic number greater than \max\{c+10k^2,100k^3\} contains a (k+1)-connected subgraph of chromatic number at least c. We prove a variant of Mader's theorem (with stronger hypotheses and a stronger conclusion), and we improve the bound in the theorem of Alon et al. 

Given a graph G, \delta(G) is the minimum degree of G. If H is an induced subgraph of G, then \partial_G(H) is the set of all vertices of H that have a neighbor in V(G) \setminus V(H). Our main results are the following two theorems. 

Theorem 1. Let k be a positive integer, and let G be a graph. If \delta_G(G) > 2k^2-1, then G contains a (k+1)-connected induced subgraph H such that \partial_G(H) \subsetneqq V(H) and |\partial_G(H)| \leq 2k^2-1. 

Theorem 2. Let k and c be positive integers, and let G be a graph such that \chi(G) > \max\{c+2k-2,2k^2\}. Then G contains a (k+1)-connected induced subgraph of chromatic number greater than c.

A {\em cut-partition} of a graph G is a partition (A,B,C) of V(G) such that A and B are non-empty (C may possibly be empty), and there are no edges between A and B. Theorem 1 is an immediate corollary of a certain technical lemma, which roughly states that if the minimum degree of a graph G is greater than 2k^2-1, then either G is (k+1)-connected, or G admits a cut-partition (A,B,C) such that G[A \cup C] is (k+1)-connected, |C| \leq 2k^2-1, and at most 2k-1 vertices of C have more than k neighbors in B. The precise statement of this lemma, as well as an outline of its proof, will be given in the talk. This lemma is also one of the main ingredients of the proof of Theorem 2. 

This is joint work with Stephan Thomasse and Nicolas Trotignon.

SLIDES